科目：czsx 来源： 题型：
| 队名 | 比赛场次 | 胜场 | 负场 | 积分 |
| 前进 | 14 | 10 | 4 | 24 |
| 东方 | 10 | 4 | 4 | 24 |
| 光明 | 14 | 9 | 5 | 23 |
| 蓝天 | 14 | 9 | 5 | 23 |
| 雄鹰 | 14 | 7 | 7 | 21 |
| 远大 | 14 | 7 | 7 | 21 |
| 卫星 | 14 | 4 | 10 | 18 |
| 钢铁 | 14 | 0 | 14 | 14 |
科目：czsx 来源： 题型：
科目：czsx 来源： 题型：
（本小题满分10分）
数形结合作为一种数学思想方法，数形结合的应用大致又可分为两种情形：或者借助于数的精确性来阐明形的某些属性，即“以数解形”；或者借助形的几何直观性来阐明数之间的某种关系，即 “以形助数”。
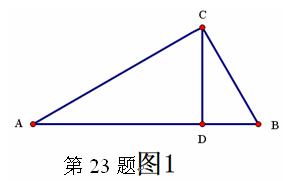
如浙教版九上课本第109页作业题第2题：如图1，已知在△ABC中，∠ACB=900，CD⊥AB，D为垂足。易证得两个结论：(1)AC·BC = AB·CD (2)AC2= AD·AB
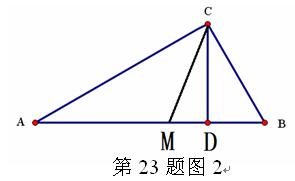
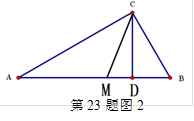
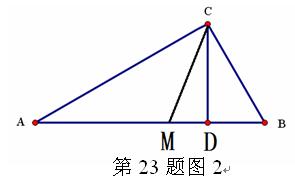
（1）请你用数形结合的“以数解形”思想来解：如图2，已知在△ABC中（AC>BC），∠ACB=900，CD⊥AB，D为垂足， CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根，求AD、MD的长。
（2）请你用数形结合的“以形助数”思想来解： 设a、b、c、d都是正数，满足a：b=c：d,且a最大。求证：a+d>b+c（提示：不访设AB=a,CD=d,AC=b,BC=c，构造图1）
科目：czsx 来源：2011-2012学年江苏扬中市九年级下学期期中考试数学试卷（解析版） 题型：解答题
运算求解（本小题满分10分）
（1）解不等式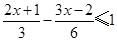
，并把它的解集在数轴上表示出来.
（2）解方程：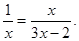
科目：czsx 来源：2012届江苏扬中市九年级下学期期中考试数学试卷（带解析） 题型：解答题
运算求解（本小题满分10分）
（1）解不等式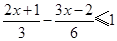
，并把它的解集在数轴上表示出来.
（2）解方程：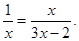
科目：czsx 来源： 题型：
科目：czsx 来源：2011学年河北省考模拟考试数学卷 题型：选择题
（本小题满分10分）
数形结合作为一种数学思想方法，数形结合的应用大致又可分为两种情形：或者借助于数的精确性来阐明形的某些属性，即 “以数解形”；或者借助形的几何直观性来阐明数之间的某种关系，即 “以形助数”。
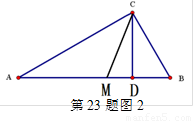如浙教版九上课本第109页作业题第2题：如图1，已知在△ABC中，∠ACB=900，CD⊥AB，D为垂足。易证得两个结论：(1)AC·BC = AB·CD (2)AC2= AD·AB
（1）请你用数形结合的“以数解形”思想来解：如图2，已知在△ABC中（AC>BC），∠ACB=900，CD⊥AB，D为垂足， CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根，求AD、MD的长。
（2）请你用数形结合的“以形助数”思想来解： 设a、b、c、d都是正数，满足a：b=c：d,且a最大。求证：a+d>b+c（提示：不访设AB=a,CD=d,AC=b,BC=c，构造图1）
科目：czsx 来源：2011年南京市溧水县中考数学一模试卷 题型：解答题
【改编】（本小题满分10分）
数形结合作为一种数学思想方法，数形结合的应用大致又可分为两种情形：或者借助于数的精确性来阐明形的某些属性，即“以数解形”；或者借助形的
几何直观性来阐明数之间的某种关系，即“以形助数”。 如浙教版九上课本第109页作业题第2题：如图1，已知在△ABC中，∠ACB=900，CD⊥AB，D为垂足。易证得两个结论：(1)AC·BC = AB·CD (2)AC2= AD·AB
（1）请你用数形结合的“以数解形”思想来解：如图2，已知在△ABC中（AC>BC），∠ACB=900，CD⊥AB，D为垂足， CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根，求AD、MD的长。
（2）请你用数形结合的“以形助数”思想来解：设a、b、c、d都是正数，满足a：b=c：d,且a最大。求证：a+d>b+c（提示：不访设AB=a,CD=d,AC=b,BC=c，构造图1）
； 
