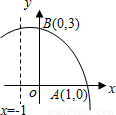如图抛物线y=x2+bx+c交y轴与B.对称轴是x=2答案解析
科目:czsx
来源:
题型:
抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:czsx
来源:
题型:
抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列结论:
①4ac﹣b2<0;
②若点(x1,y1)在抛物线上,且x1≠﹣1,则有a﹣ax12>bx1+b;
③a+b+c<0;
④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,
其中正确结论的个数是( )


A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:czsx
来源:2016届天津河西区中考模拟(三)数学试卷(解析版)
题型:选择题
抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:czsx
来源:2016届江西九年级第七次联考数学试卷(解析版)
题型:选择题
抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列结论中不正确的是( )

A.4ac﹣b2<0
B.2a﹣b=0
C.a+b+c<0
D.点(x1,y1)、(x2,y2)在抛物线上,若x1<x2,则y1<y2
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=x
2+bx+c交y轴于点A,点A关于抛物线对称轴的对称点为B(3,-4),直线y=
x与抛物线在第一象限的交点为C,连接OB.
(1)填空:b=
,c=
;
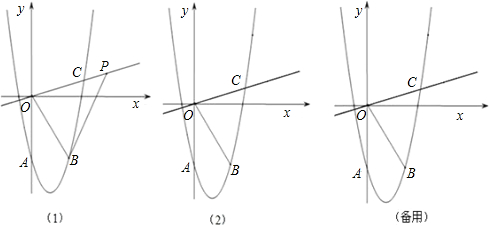
(2)如图(1),点P为射线OC上的动点,连接BP,设点P的横坐标为x,△OBP的面积为S,求S关于x的函数关系式;
(3)如图(2),点P在直线OC上的运动,点Q在抛物线上运动,问是否存在P、Q,使得以O,B,P,Q为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
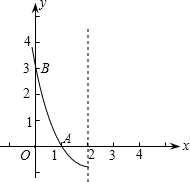
已知抛物线y=ax
2+bx+c(a≠0)的对称轴经过(2,0),且与y轴平行,抛物线与x轴相交于A(1,0),与y轴相交于B(0,3),其在对称轴左侧的图象如图所示,下面四个结论:
①x>2时,y随x的增大而增大;
②y=3时,x的值只能为0;
③若方程ax
2+bx+c=0的两根为x
1、x
2,则|x
1-x
2|=2;
④抛物线的顶点坐标是(2,-1).
正确的个数为( )
查看答案和解析>>
科目:czsx
来源:
题型:单选题
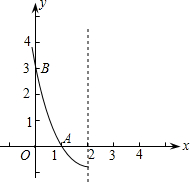 已知抛物线y=ax2+bx+c(a≠0)的对称轴经过(2,0),且与y轴平行,抛物线与x轴相交于A(1,0),与y轴相交于B(0,3),其在对称轴左侧的图象如图所示,下面四个结论:
已知抛物线y=ax2+bx+c(a≠0)的对称轴经过(2,0),且与y轴平行,抛物线与x轴相交于A(1,0),与y轴相交于B(0,3),其在对称轴左侧的图象如图所示,下面四个结论:
①x>2时,y随x的增大而增大;
②y=3时,x的值只能为0;
③若方程ax2+bx+c=0的两根为x1、x2,则|x1-x2|=2;
④抛物线的顶点坐标是(2,-1).
正确的个数为
- A.
1
- B.
2
- C.
3
- D.
4
查看答案和解析>>
科目:czsx
来源:
题型:解答题
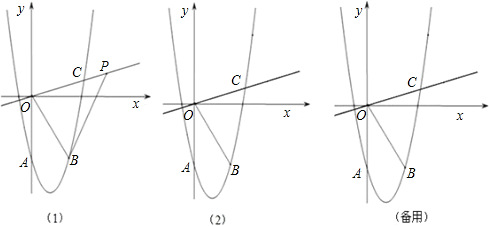
已知抛物线y=x2+bx+c交y轴于点A,点A关于抛物线对称轴的对称点为B(3,-4),直线y= x与抛物线在第一象限的交点为C,连接OB.
x与抛物线在第一象限的交点为C,连接OB.
(1)填空:b=______,c=______;
(2)如图(1),点P为射线OC上的动点,连接BP,设点P的横坐标为x,△OBP的面积为S,求S关于x的函数关系式;
(3)如图(2),点P在直线OC上的运动,点Q在抛物线上运动,问是否存在P、Q,使得以O,B,P,Q为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2012年广东省深圳市中考数学仿真模拟试卷(三)(解析版)
题型:解答题
已知抛物线y=x
2+bx+c交y轴于点A,点A关于抛物线对称轴的对称点为B(3,-4),直线y=

x与抛物线在第一象限的交点为C,连接OB.
(1)填空:b=______,c=______;
(2)如图(1),点P为射线OC上的动点,连接BP,设点P的横坐标为x,△OBP的面积为S,求S关于x的函数关系式;
(3)如图(2),点P在直线OC上的运动,点Q在抛物线上运动,问是否存在P、Q,使得以O,B,P,Q为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2010年浙江省温州市苍南县钱库一中中考数学二模试卷(解析版)
题型:解答题
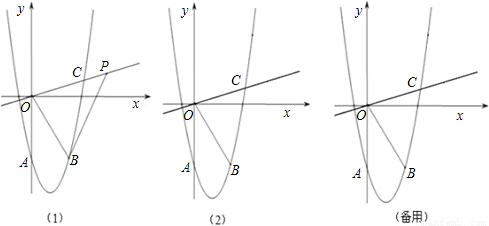
已知抛物线y=x
2+bx+c交y轴于点A,点A关于抛物线对称轴的对称点为B(3,-4),直线y=

x与抛物线在第一象限的交点为C,连接OB.
(1)填空:b=______,c=______;
(2)如图(1),点P为射线OC上的动点,连接BP,设点P的横坐标为x,△OBP的面积为S,求S关于x的函数关系式;
(3)如图(2),点P在直线OC上的运动,点Q在抛物线上运动,问是否存在P、Q,使得以O,B,P,Q为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:不详
题型:单选题
已知抛物线y=ax
2+bx+c(a≠0)的对称轴经过(2,0),且与y轴平行,抛物线与x轴相交于A(1,0),与y轴相交于B(0,3),其在对称轴左侧的图象如图所示,下面四个结论:
①x>2时,y随x的增大而增大;
②y=3时,x的值只能为0;
③若方程ax
2+bx+c=0的两根为x
1、x
2,则|x
1-x
2|=2;
④抛物线的顶点坐标是(2,-1).
正确的个数为( )

查看答案和解析>>
科目:czsx
来源:
题型:选择题
17.
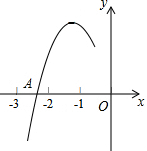
抛物线y=ax
2+bx+c(a≠0)的对称轴为直线x=-1,与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:
①4ac-b
2<0;
②若点(x
1,y
1)在抛物线上,且x
1≠-1,则有a-ax
12>bx
1+b;
③a+b+c<0;
④点M(x
1,y
1)、N(x
2,y
2)在抛物线上,若x
1<x
2,则y
1≤y
2,
其中正确结论的个数是( )
查看答案和解析>>
科目:czsx
来源:
题型:选择题
16.
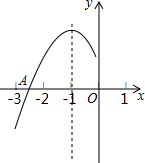
抛物线y=ax
2+bx+c(a≠0)的对称轴为直线x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论中不正确的是( )
| A. | 4ac-b2<0 |
| B. | 2a-b=0 |
| C. | a+b+c<0 |
| D. | 点(x1,y1)、(x2,y2)在抛物线上,若x1<x2,则y1<y2 |
查看答案和解析>>
科目:gzsx
来源:
题型:

如果一条抛物线y=ax
2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(Ⅰ)“抛物线三角形”一定是
三角形(提示:在答题卡上作答);
(Ⅱ)若抛物线m:y=a(x-2)
2+b(a>0,b<0)的“抛物线三角形”是直角三角形,求a,b满足的关系式;
(Ⅲ)如图,△OAB是抛物线n:y=-x
2+tx(t>0)的“抛物线三角形”,是
否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 已知抛物线y=-x2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
已知抛物线y=-x2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
(1)求抛物线的函数解析式;
(2)画出函数的图象与对称轴,设Q是抛物线的对称轴上的任意一点,以Q为圆心,QB长为半径作圆,过坐标原点O作⊙Q的切线OC,C为切点,求OC的长;
(3)特别地,要使切点C′恰好在抛物线上,应如何确定点C′的位置和圆心Q′的位置?简述你的作法并在图中把⊙Q′与切线OC′作出来(要求用尺规作图,保留作图痕迹,写作法,但不用证明).
查看答案和解析>>
科目:czsx
来源:1997年广西中考数学试卷(解析版)
题型:解答题
已知抛物线y=-x
2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
(1)求抛物线的函数解析式;
(2)画出函数的图象与对称轴,设Q是抛物线的对称轴上的任意一点,以Q为圆心,QB长为半径作圆,过坐标原点O作⊙Q的切线OC,C为切点,求OC的长;
(3)特别地,要使切点C′恰好在抛物线上,应如何确定点C′的位置和圆心Q′的位置?简述你的作法并在图中把⊙Q′与切线OC′作出来(要求用尺规作图,保留作图痕迹,写作法,但不用证明).

查看答案和解析>>
科目:czsx
来源:
题型:
(1997•广西)已知抛物线y=-x
2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
(1)求抛物线的函数解析式;
(2)画出函数的图象与对称轴,设Q是抛物线的对称轴上的任意一点,以Q为圆心,QB长为半径作圆,过坐标原点O作⊙Q的切线OC,C为切点,求OC的长;
(3)特别地,要使切点C′恰好在抛物线上,应如何确定点C′的位置和圆心Q′的位置?简述你的作法并在图中把⊙Q′与切线OC′作出来(要求用尺规作图,保留作图痕迹,写作法,但不用证明).
查看答案和解析>>
科目:czsx
来源:
题型:
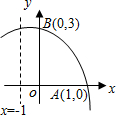
如图,函数y=-x
2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是( )
| A、顶点坐标为(-1,4) | B、函数的解析式为y=-x2-2x+3 | C、当x<0时,y随x的增大而增大 | D、抛物线与x轴的另一个交点是(-3,0) |
查看答案和解析>>
科目:czsx
来源:
题型:单选题
 如图,函数y=-x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是
如图,函数y=-x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是
- A.
顶点坐标为(-1,4)
- B.
函数的解析式为y=-x2-2x+3
- C.
当x<0时,y随x的增大而增大
- D.
抛物线与x轴的另一个交点是(-3,0)
查看答案和解析>>
科目:czsx
来源:2012年四川省南充市仪陇二中中考数学二模试卷(解析版)
题型:选择题
如图,函数y=-x
2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是( )
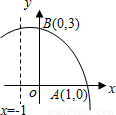
A.顶点坐标为(-1,4)
B.函数的解析式为y=-x
2-2x+3
C.当x<0时,y随x的增大而增大
D.抛物线与x轴的另一个交点是(-3,0)
查看答案和解析>>






 已知抛物线y=ax2+bx+c(a≠0)的对称轴经过(2,0),且与y轴平行,抛物线与x轴相交于A(1,0),与y轴相交于B(0,3),其在对称轴左侧的图象如图所示,下面四个结论:
已知抛物线y=ax2+bx+c(a≠0)的对称轴经过(2,0),且与y轴平行,抛物线与x轴相交于A(1,0),与y轴相交于B(0,3),其在对称轴左侧的图象如图所示,下面四个结论: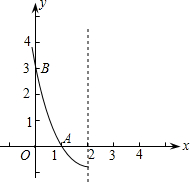 已知抛物线y=ax2+bx+c(a≠0)的对称轴经过(2,0),且与y轴平行,抛物线与x轴相交于A(1,0),与y轴相交于B(0,3),其在对称轴左侧的图象如图所示,下面四个结论:
已知抛物线y=ax2+bx+c(a≠0)的对称轴经过(2,0),且与y轴平行,抛物线与x轴相交于A(1,0),与y轴相交于B(0,3),其在对称轴左侧的图象如图所示,下面四个结论: x与抛物线在第一象限的交点为C,连接OB.
x与抛物线在第一象限的交点为C,连接OB.
 x与抛物线在第一象限的交点为C,连接OB.
x与抛物线在第一象限的交点为C,连接OB.
 x与抛物线在第一象限的交点为C,连接OB.
x与抛物线在第一象限的交点为C,连接OB.

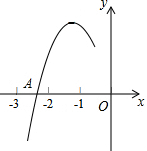 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:
抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论: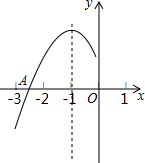 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论中不正确的是( )
抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论中不正确的是( ) 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”. 已知抛物线y=-x2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
已知抛物线y=-x2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
 (1997•广西)已知抛物线y=-x2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
(1997•广西)已知抛物线y=-x2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).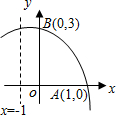 如图,函数y=-x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是( )
如图,函数y=-x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是( ) 如图,函数y=-x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是
如图,函数y=-x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是