精英家教网 >
试题搜索列表 >点P是抛物线对称轴上的一个动点.是否存在点P使△PAB的周长最小.若存在求出点P坐标.不存在说明理由△
点P是抛物线对称轴上的一个动点.是否存在点P使△PAB的周长最小.若存在求出点P坐标.不存在说明理由△答案解析
科目:czsx
来源:
题型:

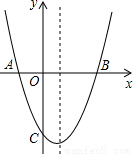
如图,已知抛物线y=x
2-2x-3与x轴交于A,B 两点.
(1)求该抛物线的顶点坐标及A、B两点的坐标;
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足
S
△PAB﹦8,并求出此时P点的坐标;
(3)设(1)中抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
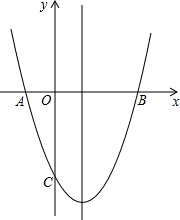 如图,已知抛物线y=x2-2x-3与x轴交于A,B 两点.
如图,已知抛物线y=x2-2x-3与x轴交于A,B 两点.
(1)求该抛物线的顶点坐标及A、B两点的坐标;
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足
S△PAB﹦8,并求出此时P点的坐标;
(3)设(1)中抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2013年四川省泸州市天立国际学校中考数学模拟试卷(二)(解析版)
题型:解答题
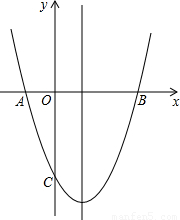
如图,已知抛物线y=x
2-2x-3与x轴交于A,B 两点.
(1)求该抛物线的顶点坐标及A、B两点的坐标;
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足
S
△PAB﹦8,并求出此时P点的坐标;
(3)设(1)中抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
2.

如图,抛物线y=x
2-bx+c与x轴交于A、C两点,与y轴交于B点,已知A点坐标为(1,0),抛物线的对称轴为直线x=2.
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)若点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:同步轻松练习 九年级数学下
题型:059
抛物线y=x2-2x-3与x轴交于A,B两点(A点在B点的左侧).
(1)抛物线上有一个动点P,求当点P在抛物线上滑动到什么位置时,△PAB的面积为10,并求出此时点P的坐标;
(2)抛物线交y轴于点C.在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,抛物线 交
交 轴于点A(1,0),交
轴于点A(1,0),交 轴于点B,对称轴是
轴于点B,对称轴是 =2.
=2.
(1)求抛物线的解析式.
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
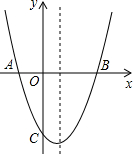
如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S
△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
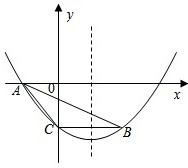
如图,抛物线
y=a(x-1)2-经过△ABC的三个顶点,已知点A(-1,0),点C在y轴上,且BC∥x轴.
(1)求a的值;
(2)判断△ABC的形状,并说明理由;
(3)探究:
①若点P是抛物线对称轴上的一个动点,求△PAC周长的最小值;
②若点P是抛物线对称轴且在直线BC上方的一个动点,是否存在点P使△PAB是等腰三角形.若存在,直接写出所有符合条件的点P坐标;不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2013年四川省泸州市高级中等学校招生考试数学
题型:044
如图,在直角坐标系中,点A的坐标为(-2,0),点B的坐标为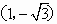 ,已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).
,已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).

(1)求抛物线的解析式;
(2)在该抛物线的对称轴上,是否存在点C,使△BOC的周长最小.若存在,求出点C的坐标.若不存在,请说明理由;
(3)如果点P是该抛物线上x轴上方的一个动点,那么△PAB是否有最大面积.若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.(注意:本题中的结果均保留根号).
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,在直角坐标系中,点A的坐标为(-2,0),点B的坐标为(1,-
如图,在直角坐标系中,点A的坐标为(-2,0),点B的坐标为(1,- ),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).
),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).
(1)求抛物线的解析式;
(2)在该抛物线的对称轴上,是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(3)如果点P是该抛物线上x轴上方的一个动点,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.(注意:本题中的结果均保留根号)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,抛物线
如图,抛物线 经过△ABC的三个顶点,已知点A(-1,0),点C在y轴上,且BC∥x轴.
经过△ABC的三个顶点,已知点A(-1,0),点C在y轴上,且BC∥x轴.
(1)求a的值;
(2)判断△ABC的形状,并说明理由;
(3)探究:
①若点P是抛物线对称轴上的一个动点,求△PAC周长的最小值;
②若点P是抛物线对称轴且在直线BC上方的一个动点,是否存在点P使△PAB是等腰三角形.若存在,直接写出所有符合条件的点P坐标;不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
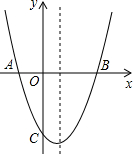 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:福建省期末题
题型:解答题
如图,抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点。
(1)求该抛物线的解析式;
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;
(3)设(1)中的抛物线交y轴于C点。在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小,若存在,求出Q点的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:czsx
来源:2012届海南省儋州市一中中考第二次模拟数学试卷(带解析)
题型:解答题
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版)
题型:解答题
如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S
△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》常考题集(26):2.3 二次函数的应用(解析版)
题型:解答题
如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S
△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:第6章《二次函数》常考题集(26):6.4 二次函数的应用(解析版)
题型:解答题
如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S
△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第27章《二次函数》常考题集(26):27.3 实践与探索(解析版)
题型:解答题
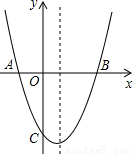
如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S
△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第26章《二次函数》常考题集(25):26.3 实际问题与二次函数(解析版)
题型:解答题
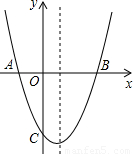
如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S
△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:九年级数学下册第26章~第27章综合检测卷(解析版)
题型:解答题
如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S
△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>

 如图,已知抛物线y=x2-2x-3与x轴交于A,B 两点.
如图,已知抛物线y=x2-2x-3与x轴交于A,B 两点. 如图,已知抛物线y=x2-2x-3与x轴交于A,B 两点.
如图,已知抛物线y=x2-2x-3与x轴交于A,B 两点.
 如图,抛物线y=x2-bx+c与x轴交于A、C两点,与y轴交于B点,已知A点坐标为(1,0),抛物线的对称轴为直线x=2.
如图,抛物线y=x2-bx+c与x轴交于A、C两点,与y轴交于B点,已知A点坐标为(1,0),抛物线的对称轴为直线x=2. 交
交 轴于点A(1,0),交
轴于点A(1,0),交 轴于点B,对称轴是
轴于点B,对称轴是 =2.
=2.
 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点. 如图,抛物线y=a(x-1)2-
如图,抛物线y=a(x-1)2-![]() ,已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).
,已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).
 如图,在直角坐标系中,点A的坐标为(-2,0),点B的坐标为(1,-
如图,在直角坐标系中,点A的坐标为(-2,0),点B的坐标为(1,- ),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).
),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点). 如图,抛物线
如图,抛物线 经过△ABC的三个顶点,已知点A(-1,0),点C在y轴上,且BC∥x轴.
经过△ABC的三个顶点,已知点A(-1,0),点C在y轴上,且BC∥x轴. 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
 与
与 轴交于A(-1,0),B(3,0) 两点.
轴交于A(-1,0),B(3,0) 两点.





