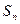科目:gzsx 来源: 题型:
| 3an |
| 2an+1 |
| 3 |
| 4 |
| p+an |
| an |
科目:gzsx 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
科目:gzsx 来源:2011年江西省抚州市教研室高二上学期期末数学理卷(A) 题型:解答题
(本小题满分14分)
已知 =2,点(
=2,点(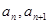 )在函数
)在函数 的图像上,其中
的图像上,其中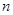 =
= .
.
(1)证明:数列 }是等比数列;
}是等比数列;
(2)设 ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式;
(3)记 ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
.
科目:gzsx 来源:2013届辽宁省高二下期中理科数学试卷(解析版) 题型:填空题
(本小题满分12分)已知数列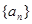 满足
满足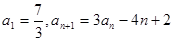 (
(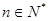 )
)
(1)求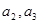 的值;
的值;
(2)证明数列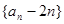 是等比数列,并求出数列
是等比数列,并求出数列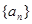 的通项公式;
的通项公式;
(3)若数列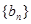 满足
满足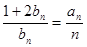 (
(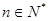 ),求数列
),求数列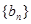 的前
的前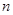 项和
项和
科目:gzsx 来源:2015届陕西省高一下学期期末考试数学试卷(解析版) 题型:解答题
已知 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
.
(1)证明:数列 }是等比数列;
}是等比数列;
(2)设 ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式;
(3)记 ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并求
,并求 的值.
的值.
科目:gzsx 来源:2010年浙江省温州二中高一第二学期期中考试数学试题 题型:解答题
(本小题满分12分)
已知点列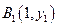 、
、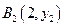 、…、
、…、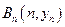 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数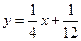 图像上的点,点列
图像上的点,点列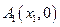 、
、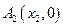 、…、
、…、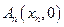 (n∈N)顺次为x轴正半轴上的点,其中
(n∈N)顺次为x轴正半轴上的点,其中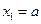 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点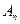 、
、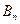 、
、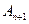 构成一个顶角的顶点为
构成一个顶角的顶点为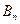 的等腰三角形。
的等腰三角形。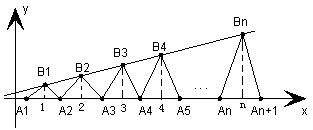
(1)数列 的通项公式,并证明
的通项公式,并证明 是等差数列;
是等差数列;
(2)证明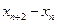 为常数,并求出数列
为常数,并求出数列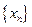 的通项公式;
的通项公式;
(3)上述等腰三角形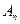
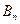
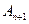 中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
科目:gzsx 来源:2013-2014学年上海市徐汇区高三上学期期末考试(一模)理科数学试卷(解析版) 题型:解答题
称满足以下两个条件的有穷数列 为
为 阶“期待数列”:
阶“期待数列”:
① ;②
;② .
.
(1)若等比数列 为
为 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及 的通项公式;
的通项公式;
(2)若一个等差数列 既是
既是 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记n阶“期待数列” 的前k项和为
的前k项和为 :
:
(i)求证: ;
;
(ii)若存在 使
使 ,试问数列
,试问数列 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
科目:gzsx 来源:2011-2012学年云南省高三11月月考理科数学 题型:解答题
(本题满分12分)已知数列 中,
中, .
.
(1)写出 的值(只写结果)并求出数列
的值(只写结果)并求出数列 的通项公式
的通项公式
(2)设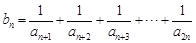 , 求
, 求 的最大值
的最大值
科目:gzsx 来源:2015届黑龙江大庆铁人中学高一4月月考数学试卷 题型:解答题
 是等比数列
是等比数列 的前
的前 项和, 公比
项和, 公比 ,已知1是
,已知1是 的等 差中项,6是
的等 差中项,6是 的等比中项,
的等比中项,
(1)求此数列的通项公式
(2)求数列 的前
的前 项和
项和
科目:gzsx 来源:2012-2013学年广东省珠海市高三9月摸底一模考试文科数学试卷(解析版) 题型:解答题
已知 ,点
,点 在函数
在函数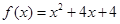 的图象上,其中
的图象上,其中
(1)证明:数列 是等比数列;
是等比数列;
(2)设数列 的前
的前 项积为
项积为 ,求
,求 及数列
及数列 的通项公式;
的通项公式;
(3)已知 是
是 与
与 的等差中项,数列
的等差中项,数列 的前
的前 项和为
项和为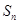 ,求证:
,求证: .
.
科目:gzsx 来源:2011年江西省抚州市教研室高二上学期期末数学理卷(A) 题型:解答题
(本小题满分14分)
已知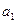 =2,点(
=2,点(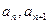 )在函数
)在函数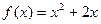 的图像上,其中
的图像上,其中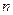 =
= .
.
(1)证明:数列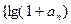 }是等比数列;
}是等比数列;
(2)设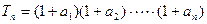 ,求
,求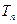 及数列{
及数列{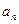 }的通项公式;
}的通项公式;
(3)记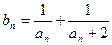 ,求数列{
,求数列{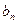 }的前n项和
}的前n项和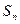 ,并证明
,并证明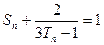 .
.
科目:gzsx 来源:2010-2011年辽宁省瓦房店市高二下学期期末联考文科数学 题型:解答题
.(本题满分12分)[
已知数列 满足
满足 (
( )
)
(1)求 的值;
的值;
(2)证明数列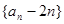 是等比数列,并求出数列
是等比数列,并求出数列 的通项公式;
的通项公式;
(3)若数列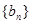 满足
满足 (
( ),求数列
),求数列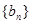 的前
的前 项和
项和
科目:gzsx 来源:2010年浙江省高一第二学期期中考试数学试题 题型:解答题
(本小题满分12分)
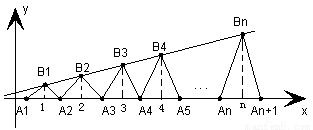
已知点列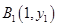 、
、 、…、
、…、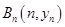 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数 图像上的点,点列
图像上的点,点列 、
、 、…、
、…、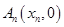 (n∈N)顺次为x轴正半轴上的点,其中
(n∈N)顺次为x轴正半轴上的点,其中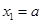 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点 、
、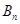 、
、 构成一个顶角的顶点为
构成一个顶角的顶点为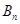 的等腰三角形。
的等腰三角形。
(1)数列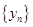 的通项公式,并证明
的通项公式,并证明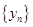 是等差数列;
是等差数列;
(2)证明 为常数,并求出数列
为常数,并求出数列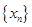 的通项公式;
的通项公式;
(3)上述等腰三角形
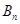
 中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
科目:gzsx 来源:2010-2011年辽宁省瓦房店市高级中学高二下学期期末联考文科数学 题型:解答题
.(本题满分12分)[
已知数列 满足
满足 (
(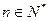 )
)
(1)求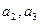 的值;
的值;
(2)证明数列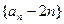 是等比数列,并求出数列
是等比数列,并求出数列 的通项公式;
的通项公式;
(3)若数列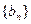 满足
满足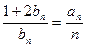 (
(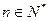 ),求数列
),求数列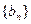 的前
的前 项和
项和