等边三角形ABC点D在直线AC上点E在直线BC上连接DE答案解析
科目:czsx
来源:
题型:解答题
8.已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作∠DAF=60°,在射线AF上截取点F,使AF=AD,过D作DE∥AF,过F作EF∥AD,DE、EF交于点E,连接CF
(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.

查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读材料:
如图1,△ABC和△CDE都是等边三角形,且点A、C、E在一条直线上,可以证明△ACD≌△BCE,则AD=BE.
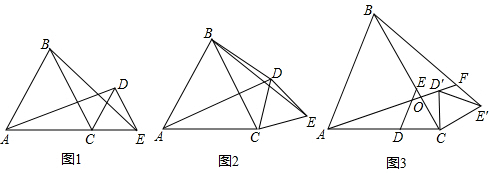
解决问题:
(1)将图1中的△CDE绕点C旋转到图2,猜想此时线段AD与BE的数量关系,并证明你的结论.
(2)如图2,连接BD,若AC=2cm,CE=1cm,现将△CDE绕点C继续旋转,则在旋转过程中,△BDE的面积是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(3)如图3,在△ABC中,点D在AC上,点E在BC上,且DE∥AB,将△DCE绕点C按顺时针方向旋转得到三角形CD′E′(使∠ACD′<180°),连接BE′,AD′,设AD′分别交BC、BE′于O、F,若△ABC满足∠ACB=60°,BC=
,AC=
,
①求
的值及∠BFA的度数;
②若D为AC的中点,求△AOC面积的最大值.
查看答案和解析>>
科目:czsx
来源:
题型:

△ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连接PQ交直线AC于点D,作PE⊥AC,垂足为E.
(1)如图,当点P在边AB(与点A、B不重合)上,问:
①线段PD与线段DQ之间有怎样的大小关系?试证明你的结论.
②随着点P、Q的移动,线段DE的长能否确定?若能,求出DE的长;若不能,简要说明理由;
(2)当点P在射线AB上,若设AP=x,CD=y,求:
①y与x之间的函数关系式,并写出x的取值范围;
②当x为何值时,△PCQ的面积与△ABC的面积相等.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
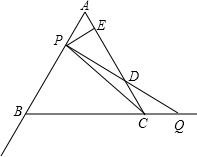 △ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连接PQ交直线AC于点D,作PE⊥AC,垂足为E.
△ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连接PQ交直线AC于点D,作PE⊥AC,垂足为E.
(1)如图,当点P在边AB(与点A、B不重合)上,问:
①线段PD与线段DQ之间有怎样的大小关系?试证明你的结论.
②随着点P、Q的移动,线段DE的长能否确定?若能,求出DE的长;若不能,简要说明理由;
(2)当点P在射线AB上,若设AP=x,CD=y,求:
①y与x之间的函数关系式,并写出x的取值范围;
②当x为何值时,△PCQ的面积与△ABC的面积相等.
查看答案和解析>>
科目:czsx
来源:2010-2011学年江苏省泰州市泰兴市实验初级中学九年级(上)阶段测试数学试卷(解析版)
题型:解答题

△ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连接PQ交直线AC于点D,作PE⊥AC,垂足为E.
(1)如图,当点P在边AB(与点A、B不重合)上,问:
①线段PD与线段DQ之间有怎样的大小关系?试证明你的结论.
②随着点P、Q的移动,线段DE的长能否确定?若能,求出DE的长;若不能,简要说明理由;
(2)当点P在射线AB上,若设AP=x,CD=y,求:
①y与x之间的函数关系式,并写出x的取值范围;
②当x为何值时,△PCQ的面积与△ABC的面积相等.
查看答案和解析>>
科目:gzsx
来源:
题型:
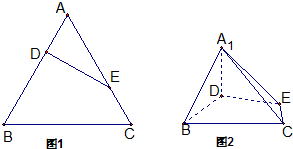
等边三角形ABC的边长为3,点D,、E分别是边AB、AC上的点,且满足
=
=
.将△ADE沿DE折起到△A
1DE的位置,使二面角A
1-DE-B成直二面角,连接A
1B、A
1C.
(1)求证:A
1D⊥平面BCED;
(2)求A
1E与平面A
1BC所成角的正弦值.
(3)在线段BC上是否存在点P,使直线PA
1与平面A
1BD所成的角为60°?若存在,求出PB的长;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
等边三角形ABC的边长为3,点D,E分别是边AB,AC上的点,且满足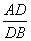 =
= =
= (如图①).将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B为直二面角,连接A1B,A1C(如图②).
(如图①).将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B为直二面角,连接A1B,A1C(如图②).
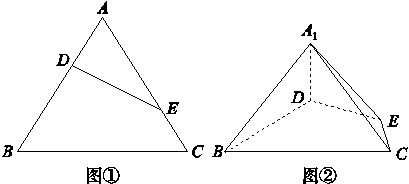
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60°?若存在,求出PB的长,若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=
,BC=1.连接BF,分别交AC、DC、DE于点P、Q、R.
(1)求证:△BFG∽△FEG;
(2)求出BF的长;
(3)求
=
(直接写出结果).
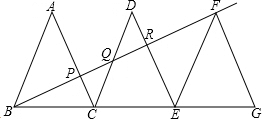
查看答案和解析>>
科目:czsx
来源:
题型:解答题
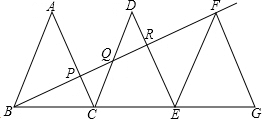
已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB= ,BC=1.连接BF,分别交AC、DC、DE于点P、Q、R.
,BC=1.连接BF,分别交AC、DC、DE于点P、Q、R.
(1)求证:△BFG∽△FEG;
(2)求出BF的长;
(3)求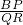 =______(直接写出结果).
=______(直接写出结果).
查看答案和解析>>
科目:czsx
来源:学习周报 数学 沪科九年级版 2009-2010学年 第6期 总第162期 沪科版
题型:047
如图,△
ABC
、△DCE
、△FEG
是三个全等的等腰三角形,底边BC
、CE
、EG
在同一直线上,且AB
=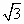 ,
,BC
=1
,连接BF
,分别交AC
、DC
、DE
于点P
、Q
、R
.

求证:△
BFG
∽△FEG
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,在等边三角形ABC中,点D的是射线AB上一点,点E是射线AC上一点,连接DE交BC于F,BD=CE,易证:BF+BD=CF.
如图2,在等腰直角三角形ABC中,上述条件仍然成立,那么BF,BD和CF之间有怎样的数量关系?请直接写出你的猜想;
如图3,在等腰△ABC中,AB=AC,∠A=120°,其它条件仍然成立,那么BF,BD和CF之间有怎样的数量关系?并对你的结论进行证明.

查看答案和解析>>
科目:czsx
来源:
题型:
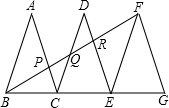
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=
,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
(1)求证:△BFG∽△FEG,并求出BF的长;
(2)观察图形,请你提出一个与点P相关的问题,并进行解答.(根据提出问题的层次和解答过程评分)
查看答案和解析>>
科目:czsx
来源:
题型:
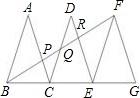
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=
,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC;②BQ=FQ;③AP=2PC;④EF平分∠BFG,你认为不正确的是( )
查看答案和解析>>
科目:czsx
来源:活学巧练 八年级数学 下
题型:044
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=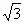 ,BC=1.连接BF,分别交AC、DC、DE于点P、Q、R.
,BC=1.连接BF,分别交AC、DC、DE于点P、Q、R.

(1)求证:△BFG∽△FEG,并求出BF的长;
(2)观察图形,请你提出一个与点P相关的问题,并进行解答(根据提出问题的层次和解答过程评分).
查看答案和解析>>
科目:czsx
来源:
题型:单选题
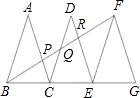 如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB= ,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC;②BQ=FQ;③AP=2PC;④EF平分∠BFG,你认为不正确的是
,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC;②BQ=FQ;③AP=2PC;④EF平分∠BFG,你认为不正确的是
- A.
①②
- B.
②③
- C.
③④
- D.
④
查看答案和解析>>
科目:czsx
来源:《第27章 相似》2010年整章同步测试(解析版)
题型:解答题
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=
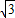
,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
(1)求证:△BFG∽△FEG,并求出BF的长;
(2)观察图形,请你提出一个与点P相关的问题,并进行解答.(根据提出问题的层次和解答过程评分)
查看答案和解析>>
科目:czsx
来源:《第27章 相似》2010年整章测试(解析版)
题型:解答题
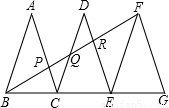
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=

,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
(1)求证:△BFG∽△FEG,并求出BF的长;
(2)观察图形,请你提出一个与点P相关的问题,并进行解答.(根据提出问题的层次和解答过程评分)

查看答案和解析>>
科目:czsx
来源:《24.3.2 相似三角形的判定》2010年同步练习2(解析版)
题型:解答题
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=

,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
(1)求证:△BFG∽△FEG,并求出BF的长;
(2)观察图形,请你提出一个与点P相关的问题,并进行解答.(根据提出问题的层次和解答过程评分)

查看答案和解析>>
科目:czsx
来源:第19章《相似形》常考题集(08):19.5 相似三角形的判定(解析版)
题型:解答题
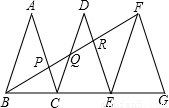
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=

,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
(1)求证:△BFG∽△FEG,并求出BF的长;
(2)观察图形,请你提出一个与点P相关的问题,并进行解答.(根据提出问题的层次和解答过程评分)
查看答案和解析>>
科目:czsx
来源:第29章《相似形》常考题集(06):29.4 三角形相似的条件(解析版)
题型:解答题
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=

,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
(1)求证:△BFG∽△FEG,并求出BF的长;
(2)观察图形,请你提出一个与点P相关的问题,并进行解答.(根据提出问题的层次和解答过程评分)

查看答案和解析>>



 △ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连接PQ交直线AC于点D,作PE⊥AC,垂足为E.
△ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连接PQ交直线AC于点D,作PE⊥AC,垂足为E. △ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连接PQ交直线AC于点D,作PE⊥AC,垂足为E.
△ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连接PQ交直线AC于点D,作PE⊥AC,垂足为E. △ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连接PQ交直线AC于点D,作PE⊥AC,垂足为E.
△ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连接PQ交直线AC于点D,作PE⊥AC,垂足为E.
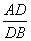 =
= =
= (如图①).将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B为直二面角,连接A1B,A1C(如图②).
(如图①).将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B为直二面角,连接A1B,A1C(如图②).

 ,BC=1.连接BF,分别交AC、DC、DE于点P、Q、R.
,BC=1.连接BF,分别交AC、DC、DE于点P、Q、R.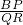 =______(直接写出结果).
=______(直接写出结果).



 如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=![]() ,BC=1.连接BF,分别交AC、DC、DE于点P、Q、R.
,BC=1.连接BF,分别交AC、DC、DE于点P、Q、R.
 如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB= ,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC;②BQ=FQ;③AP=2PC;④EF平分∠BFG,你认为不正确的是
,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC;②BQ=FQ;③AP=2PC;④EF平分∠BFG,你认为不正确的是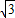 ,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
 ,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
 ,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
 ,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
 ,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.
,BC=1,连接BF,分别交AC、DC、DE于点P、Q、R.