科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
问题情境:
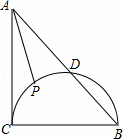
如图1,P是⊙O外的一点,直线PO分别交⊙O于点A、B,则PA是点P到⊙O上的点的最短距离.

探究:
请您结合图2给予证明,
归纳:
圆外一点到圆上各点的最短距离是:这点到连接这点与圆心连线与圆交点之间的距离.
图中有圆,直接运用:
如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是 上的一个动点,连接AP,则AP的最小值是 .
上的一个动点,连接AP,则AP的最小值是 .
|
图中无圆,构造运用:
如图4,在边长为2的菱形 中,∠
中,∠ =60°,
=60°, 是
是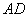 边的中点,
边的中点,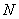 是
是 边上一动点,将△
边上一动点,将△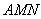 沿
沿 所在的直线翻折得到△
所在的直线翻折得到△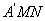 ,连接
,连接 ,请求出
,请求出 长度的最小
长度的最小
值.

 | |||
|
解:由折叠知 ,又M是AD的中点,可得
,又M是AD的中点,可得 ,故点
,故点 在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
迁移拓展,深化运用:
如图6,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .

|
科目:czsx 来源:2014-2015学年江苏省东台市九年级下学期第一次质量检测数学试卷(解析版) 题型:解答题
问题情境:如图1,P是⊙O外的一点,直线PO分别交⊙O于点A、B,则PA是点P到⊙O上的点的最短距离.

探究:
请您结合图2给予证明,
归纳:
圆外一点到圆上各点的最短距离是:这点到连接这点与圆心连线与圆交点之间的距离.
图中有圆,直接运用:
如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是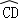 上的一个动点,连接AP,则AP的最小值是 .
上的一个动点,连接AP,则AP的最小值是 .

图中无圆,构造运用:
如图4,在边长为2的菱形 中,∠
中,∠ =60°,
=60°,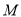 是
是 边的中点,
边的中点, 是
是 边上一动点,将△
边上一动点,将△ 沿
沿 所在的直线翻折得到△
所在的直线翻折得到△ ,连接
,连接 ,请求出
,请求出 长度的最小
长度的最小
值.

【解析】
由折叠知 ,又M是AD的中点,可得
,又M是AD的中点,可得 ,故点
,故点 在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
迁移拓展,深化运用:
如图6,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .

科目:czsx 来源:2015-2016学年河北省保定市涞水县八年级上学期期末数学试卷(解析版) 题型:解答题
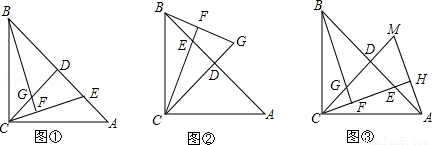
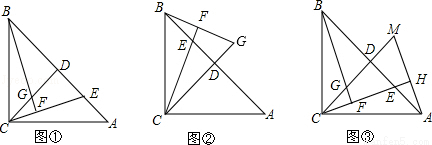
(2015秋•涞水县期末)已知:在△ABC中,AC=BC,∠ACB=90°,过点C作CD⊥AB于点D,点E是AB边上一动点(不含端点A、B),连接CE,过点B作CE的垂线交直线CE于点F,交直线CD于点G(如图①).
(1)求证:AE=CG;
(2)若点E运动到线段BD上时(如图②),试猜想AE、CG的数量关系是否发生变化,请直接写出你的结论;
(3)过点A作AH垂直于直线CE,垂足为点H,并交CD的延长线于点M(如图③),找出图中与BE相等的线段,并证明.
科目:czsx 来源:2015-2016学年江苏省八年级上第一次月考数学卷(解析版) 题型:解答题
(2015秋•涞水县期末)已知:在△ABC中,AC=BC,∠ACB=90°,过点C作CD⊥AB于点D,点E是AB边上一动点(不含端点A、B),连接CE,过点B作CE的垂线交直线CE于点F,交直线CD于点G(如图①).
(1)求证:AE=CG;
(2)若点E运动到线段BD上时(如图②),试猜想AE、CG的数量关系是否发生变化,请直接写出你的结论;
(3)过点A作AH垂直于直线CE,垂足为点H,并交CD的延长线于点M(如图③),找出图中与BE相等的线段,并证明.