
科目:czsx 来源: 题型:
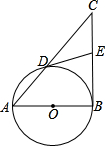 如图,以Rt△ABC的直角边AB为直径作圆O与斜边AC交于点D,E为BC边的中点,连接DE.
如图,以Rt△ABC的直角边AB为直径作圆O与斜边AC交于点D,E为BC边的中点,连接DE.科目:czsx 来源: 题型:解答题
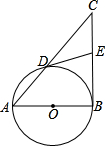 如图,以Rt△ABC的直角边AB为直径作圆O与斜边AC交于点D,E为BC边的中点,连接DE.
如图,以Rt△ABC的直角边AB为直径作圆O与斜边AC交于点D,E为BC边的中点,连接DE.科目:czsx 来源:2009年广东省深圳市实验中学中考数学模拟试卷(解析版) 题型:解答题
科目:czsx 来源: 题型:单选题
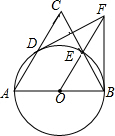 如图,等腰三角形ABC,AB=AC,以AB为直径作圆O分别交AC、BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:①
如图,等腰三角形ABC,AB=AC,以AB为直径作圆O分别交AC、BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:①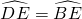 ,②FD是⊙O的切线;③∠C=∠DFB;④E是△BDF的内心.
,②FD是⊙O的切线;③∠C=∠DFB;④E是△BDF的内心.科目:czsx 来源: 题型:
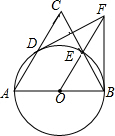 如图,等腰三角形ABC,AB=AC,以AB为直径作圆O分别交AC、BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:①
如图,等腰三角形ABC,AB=AC,以AB为直径作圆O分别交AC、BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:① |
| DE |
 |
| BE |
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
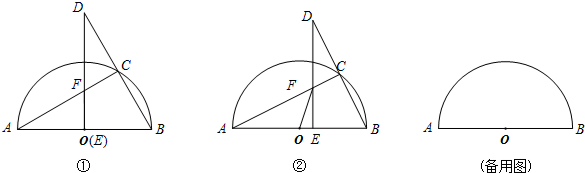
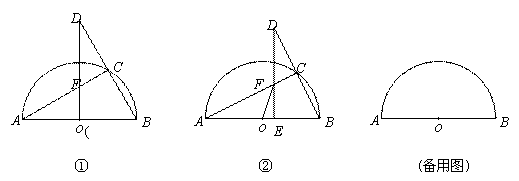
以AB为直径作半圆O,AB=10,点![]() C是该半圆上一动点,联结AC、BC,并延长BC至点D,使DC=BC,过点D作DE⊥AB于点E、交AC于点F,联结OF.
C是该半圆上一动点,联结AC、BC,并延长BC至点D,使DC=BC,过点D作DE⊥AB于点E、交AC于点F,联结OF.
(1)如图①,当点E与点O重合时,求∠BAC的度数;
(2)如图②,当DE=8时,求线段EF的长;
(3)在点C运动过程中,若点E始终在线段AB上,是否存在以点E、O、F为顶点的三角形与△ABC相似,若存在,请直接写出此时线段OE的长;若不存在,请说明理由.
 |
科目:czsx 来源: 题型:

科目:czsx 来源:2013年贵州省毕节地区高级中等学校招生考试数学 题型:013
在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则⊙O的半径和∠MND的度数分别为
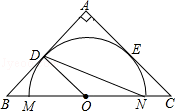
A.2,22.5°
B.3,30°
C.3,22.5°
D.2,30°
科目:czsx 来源:2013年贵州省黔东南高级中等学校招生考试数学 题型:044
如图,在直角三角形ABC中,∠ABC=90°.

(1)先作∠ACB的平分线;设它交AB边于点O,再以点O为圆心,OB为半径作⊙O(尺规作图,保留作图痕迹,不写作法);
(2)证明:AC是所作⊙O的切线;
(3)若BC=![]() ,sinA=
,sinA=![]() ,求△AOC的面积.
,求△AOC的面积.
科目:czsx 来源:2007年山东省泰安市中考真题数学试卷(非课改区) 题型:044
如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC,垂足为F.
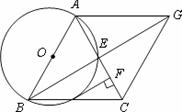
(1)求证:DF为⊙O的切线;
(2)若过A点且与BC平行的直线交BE的延长线于G点,连结CG.当△ABC是等边三角形时,求∠AGC的度数.
科目:czsx 来源: 题型:
如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC,垂足为F.
(1)判断直线DF与⊙O的位置关系,并说明理由.
(2)若过A点且与BC平行的直线交BE的延长线于G点,连结CG.当△ABC是等边三角形时,求∠AGC的度数.

科目:czsx 来源:数学教研室 题型:044

科目:czsx 来源: 题型:
如图,等边三角形ABC边长为4,E是边BC上一动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB,设EC=![]() (0<
(0<![]() ≤2).
≤2).
(1)请直接写出图中与线段EF相等的两条线段(不再另外添加辅助线)。
(2)Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求□EFPQ的面积(用含![]() 的代数式表示)?
的代数式表示)?
(3)当(2)中的平行四边形面积最大时,以E为圆心,![]() 为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应
为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应![]() 的取值范围
的取值范围
科目:czsx 来源: 题型:
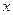 (0<
(0<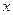 ≤2).
≤2).
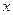 的代数式表示)?
的代数式表示)? 为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应
为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应 的取值范围
的取值范围 科目:czsx 来源:2010年湖北省黄冈市初二上学期期末数学卷 题型:解答题
如图,等边三角形ABC边长为4,E是边BC上一动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB,设EC= (0<
(0< ≤2).
≤2).
(1)请直接写出图中与线段EF相等的两条线段(不再另外添加辅助线)。
(2)Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求□EFPQ的面积(用含 的代数式表示)?
的代数式表示)?
(3)当(2)中的平行四边形面积最大时,以E为圆心, 为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应
为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应 的取值范围
的取值范围
科目:czsx 来源:2010年湖北省黄冈市初二上学期期末数学卷 题型:解答题
如图,等边三角形ABC边长为4,E是边BC上一动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB,设EC= (0<
(0< ≤2).
≤2).
(1)请直接写出图中与线段EF相等的两条线段(不再另外添加辅助线)。
(2)Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求□EFPQ的面积(用含 的代数式表示)?
的代数式表示)?
(3)当(2)中的平行四边形面积最大时,以E为圆心,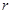 为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应
为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应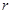 的取值范围
的取值范围
科目:czsx 来源: 题型:
张华与李明在讨论问题:“已知线段a、b,求作Rt△ABC,使∠C=90°,AB=a,AC=b”时,提出了如下的画法:1、画线段AB=a;2、以AB为直径画⊙O;3、以A为圆心,b为半径画圆与⊙O交于点C,连接BC,则△ABC为所求作的三角形.
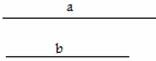

问题1:在张华的画法中,他应用了什么知识得到∠C=90°的?
答:
问题2:已知△ABC中,∠ACB=90°,AC=BC=2,P、Q分别是边AB、BC上的动点,且点P不与A、B重合,点Q不与B、C重合,当CQ的长取不同的值时,
△CPQ是否可能为直角三角形?若可能,请求出CQ的范围;若不能,说明理由.

科目:czsx 来源:2013届江苏扬州市宝应县九年级中考网上阅卷适应性调研(二模)数学试卷(带解析) 题型:解答题
在直角三角形ABC中,∠ACB=90°,AC=6,BC=8,O为AB上一点,OA=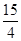 ,以O为圆心,OA为半径作圆.
,以O为圆心,OA为半径作圆.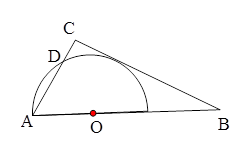
(1)试判断⊙O与BC的位置关系,并说明理由;
(2)若⊙O与AC交于另一点D,求CD的长.
科目:czsx 来源:2012-2013学年江苏扬州市宝应县九年级中考网上阅卷适应性调研(二模)数学试卷(解析版) 题型:解答题
在直角三角形ABC中,∠ACB=90°,AC=6,BC=8,O为AB上一点,OA= ,以O为圆心,OA为半径作圆.
,以O为圆心,OA为半径作圆.
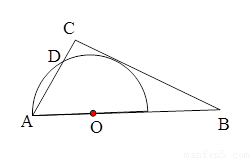
(1)试判断⊙O与BC的位置关系,并说明理由;
(2)若⊙O与AC交于另一点D,求CD的长.