
科目:czsx 来源: 题型:
如图,AB是⊙O的直径,CB、CE分别切⊙O于点B、D,CE与BA的延长线交于点E,连结OC、OD.
⑴求证:△OBC≌△ODC;
⑵已知DE=a,AE=b,BC=c,请你思考后,选用以上适当的数(两个或三个)作为已知量,设计出计算⊙O半径r的一种方案:
①你选用的已知数是 ;
②写出求解过程.(结果用字母表示)

科目:czsx 来源:数学教研室 题型:044
有一个著名的希波克拉蒂月牙问题,如图,以AB为直径作半圆,C是圆弧上一点(不与A,B重合),以AC,BC为直径分别作半圆,围成两个月牙形Ⅰ,Ⅱ(阴影部分),已知直径AC为4,直径BC为3,直径AB为5,请你猜测,这两个月牙形的面积与△ABC的面积之间有何等量关系?请说明理由.

科目:czsx 来源:数学教研室 题型:044
有一人著名的希波拉克底月牙问题,如图:以AB为直径作半圆,C是圆弧上一点(不与A、B重合),以AC、BC为直径分作半圆,围成两个月牙形Ⅰ、Ⅱ(阴影部分).已知直径AC为4,直径为BC为3,直径AB为5,求:
(1)分别求出三个半圆的面积;
(2)请你猜测:这两个月牙形(Ⅰ、Ⅱ)的面积与△ABC的面积之间有何等量关系?试写出来.

科目:czsx 来源: 题型:044
有一个著名的希波克拉蒂月牙问题,如图,以AB为直径作半圆,C是圆弧上一点(不与A,B重合),以AC,BC为直径分别作半圆,围成两个月牙形Ⅰ,Ⅱ(阴影部分),已知直径AC为4,直径BC为3,直径AB为5,请你猜测,这两个月牙形的面积与△ABC的面积之间有何等量关系?请说明理由.

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2007年上海市宝山区中考数学二模试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
 -2,0),C(m,0),其中m>0.以OB,OC为直径的圆分别交AB于点E,交AC于点F,连接EF.
-2,0),C(m,0),其中m>0.以OB,OC为直径的圆分别交AB于点E,交AC于点F,连接EF.| 3 |
| 3 |
科目:czsx 来源: 题型:
 OE,CD=
OE,CD=| 3 |
科目:czsx 来源: 题型:
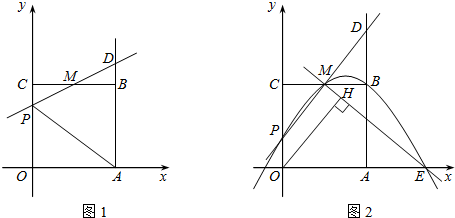
科目:czsx 来源:课堂三级讲练数学九年级(上) 题型:044
如图,在平面直角坐标系中,已知△ABC的顶点坐标分别为A(0,3)、B(-2,0)、C(m,0),其中m>0,以OB、OC为直径的圆分别交AB于点E,交AC于点F,连结EF.

(1)求证:△AFE∽△ABC;
(2)是否存在m的值,使得△AEF是等腰三角形?若存在,求出m的值;若不存在,请说明理由;
(3)观察当点C在x轴上移动时,点F移动变化的情况,试求点C从点C1(![]() ,0)移动到点C2(3
,0)移动到点C2(3![]() ,0)时,点F移动的行程.
,0)时,点F移动的行程.
科目:czsx 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:022
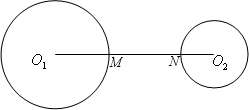
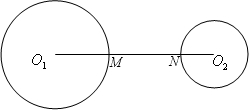
如图,已知AD=30,点B,C是AD上的三等分点,分别以AB,BC,CD为直径作圆,圆心分别为E,F,G,AP切⊙G于点P,交⊙F于M,N,则弦MN的长是________.

科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
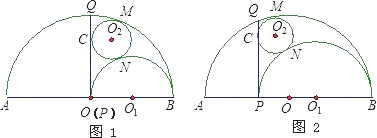
如图1,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一个动点(点C除外),直线PM交AB的延长线于点D.
1.求点D的坐标(用含m的代数式表示);
2.当△ADP是等腰三角形时,求m的值;
3.设过点P、M、B的抛物线与x轴的正半轴交于点E,过点O作直线ME的垂线,垂足为H(如图2).当点P从原点O向点C运动时,点H也随之运动.请直接写出点H所经过的路径长(不写解答过程).
科目:czsx 来源: 题型:
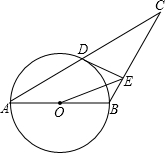
如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连结OE,CD=![]() ,∠ACB=30°.
,∠ACB=30°.
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为 .
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
 ,∠ACB=30°.
,∠ACB=30°.
科目:czsx 来源:2012届江苏省苏州市草桥中学九年级中考二模数学试卷(带解析) 题型:解答题
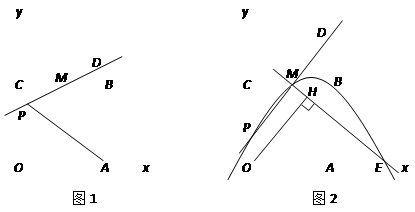
如图1,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一个动点(点C除外),直线PM交AB的延长线于点D.
【小题1】求点D的坐标(用含m的代数式表示);
【小题2】当△ADP是等腰三角形时,求m的值;
【小题3】设过点P、M、B的抛物线与x轴的正半轴交于点E,过点O作直线ME的垂线,垂足为H(如图2).当点P从原点O向点C运动时,点H也随之运动.请直接写出点H所经过的路径长(不写解答过程).
科目:czsx 来源:2010年高级中等学校招生全国统一考试数学卷(河北) 题型:解答题
如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连结OE,CD=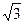 ,∠ACB=30°.
,∠ACB=30°.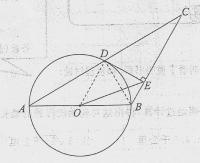
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为 .