
科目:czsx 来源: 题型:
 如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.
如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.| 2 |
| 3 |
科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
| 3 |
| 3 |
科目:czsx 来源: 题型:解答题
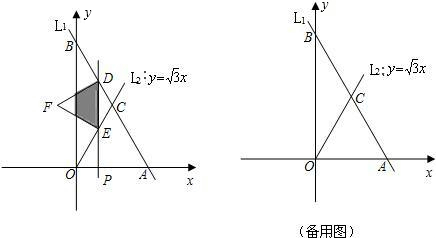
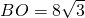 ,与直线
,与直线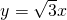 交于点C.平行于y轴的直线L2从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;l2分别交线段BC、OC、x轴于点D、E、P,以DE为边向左侧作等边△DEF,设直线l2的运动时间为t(秒).
交于点C.平行于y轴的直线L2从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;l2分别交线段BC、OC、x轴于点D、E、P,以DE为边向左侧作等边△DEF,设直线l2的运动时间为t(秒).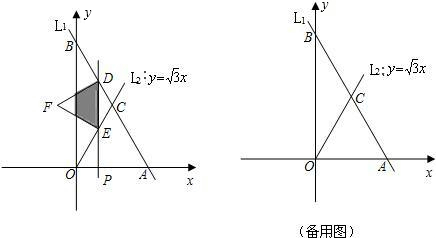
科目:czsx 来源:2011年福建省泉州市泉港区初中学业质量检查数学试卷(解析版) 题型:解答题
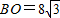 ,与直线
,与直线 交于点C.平行于y轴的直线L2从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;l2分别交线段BC、OC、x轴于点D、E、P,以DE为边向左侧作等边△DEF,设直线l2的运动时间为t(秒).
交于点C.平行于y轴的直线L2从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;l2分别交线段BC、OC、x轴于点D、E、P,以DE为边向左侧作等边△DEF,设直线l2的运动时间为t(秒).
科目:czsx 来源:福建省模拟题 题型:解答题
 ,与直线y=
,与直线y= x交于点C,平行于y轴的直线l2从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;l2分别交线段BC、OC、x轴于点D、E、P,以DE为边向左侧作等边△DEF,设直线l2的运动时间为t(秒)。
x交于点C,平行于y轴的直线l2从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;l2分别交线段BC、OC、x轴于点D、E、P,以DE为边向左侧作等边△DEF,设直线l2的运动时间为t(秒)。
科目:czsx 来源: 题型:
如图1,一条抛物线与 轴交于A,B两点(点A在点B的左侧),与
轴交于A,B两点(点A在点B的左侧),与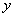 轴交于点C,且当x=-1和x=3时,
轴交于点C,且当x=-1和x=3时,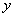 的值相等.直线
的值相等.直线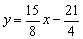 与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
(1)求这条抛物线的表达式.
(2)动点P从原点O出发,在线段OB上以每秒1个单位长度的速度向点B运动,同时动点Q从点B出发,在线段BC上以每秒 2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为
2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为 秒.
秒.
①若使△BPQ为直角三角形,请求出所有符合条件的 值;
值;
②求 为何值时,四边形ACQ P的面积有最小值,最小值是多少?
为何值时,四边形ACQ P的面积有最小值,最小值是多少?
(3)如图2,当动点P运动到OB的中点时,过点P作PD⊥ 轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿
轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿 轴向左平移
轴向左平移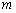 个单位长度(
个单位长度(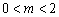 ),将平移后的三角形与△ODM重叠部分的面积记为
),将平移后的三角形与△ODM重叠部分的面积记为 ,求
,求 与
与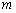 的函数关系式.
的函数关系式.
 |
科目:czsx 来源:2015年初中毕业升学考试(辽宁营口卷)数学(解析版) 题型:解答题
如图1,一条抛物线与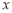 轴交于A,B两点(点A在点B的左侧),与
轴交于A,B两点(点A在点B的左侧),与 轴交于点C,且当x=-1和x=3时,
轴交于点C,且当x=-1和x=3时,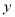 的值相等.直线
的值相等.直线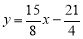 与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
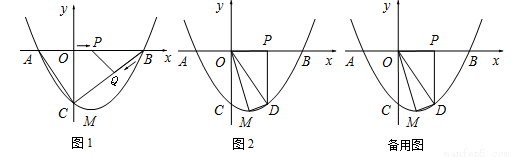
(1)求这条抛物线的表达式.
(2)动点P从原点O出发,在线段OB上以每秒1个单位长度的速度向点B运动,同时动点Q从点B出发,在线段BC上以每秒2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为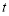 秒.
秒.
①若使△BPQ为直角三角形,请求出所有符合条件的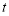 值;
值;
②求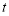 为何值时,四边形ACQ P的面积有最小值,最小值是多少?
为何值时,四边形ACQ P的面积有最小值,最小值是多少?
(3)如图2,当动点P运动到OB的中点时,过点P作PD⊥ 轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿
轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿 轴向左平移
轴向左平移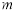 个单位长度(
个单位长度( ),将平移后的三角形与△ODM重叠部分的面积记为
),将平移后的三角形与△ODM重叠部分的面积记为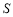 ,求
,求 与
与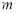 的函数关系式.
的函数关系式.
科目:gzwl 来源: 题型:
如图30-12所示,在y轴右方有一垂直纸面向里的匀强磁场,磁感应强度B=0.20 T.有一质子以速度v=2.0×106 m/s,从x轴上的A点沿与x轴正方向成30°角斜向上射入磁场.质子质量m=1.6×10-27 kg,电荷量q=1.6×10-19 C,质子重力不计.求:

图30-12
(1)质子在磁场中做圆周运动的半径;
(2)若质子能沿x轴负方向通过y轴上的C点,如图30-12所示,求C 点离坐标原点的距离.
(3)在y轴左侧存在水平向右的匀强电场,场强大小E=105 N/C,求质子从A点出发至速度第一次为零所用的时间.(结果保留两位有效数字)
科目:czsx 来源:2012届广东省惠州市惠城区十一校九年级上学期期末联考数学卷 题型:解答题
一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1
个单位.用实数加法表示为 3+(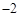 )=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移
)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移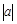 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移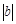 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
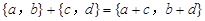 .
.
(1)计算:{3,1}+{1,2};
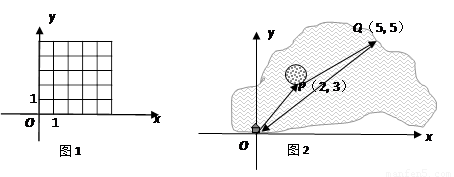
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点O吗? 在图1中画出四边形OABC.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
科目:czsx 来源: 题型:
一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1
个单位.用实数加法表示为 3+(![]() )=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移
)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移![]() 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移![]() 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为![]() .
.
(1)计算:{3,1}+{1,2};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点O吗? 在图1中画出四边形OABC.
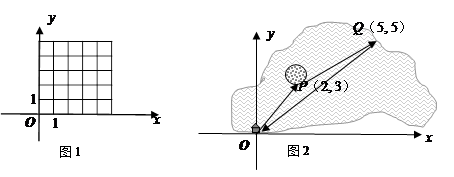
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
科目:czsx 来源: 题型:
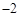 )=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移
)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移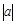 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移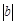 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 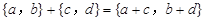 .
.
科目:czsx 来源: 题型:
一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(-2 )=1.
)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.

解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1};
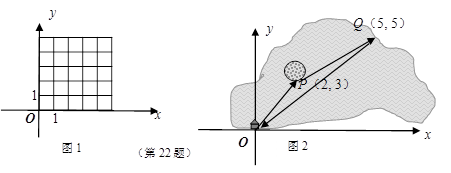
(2)动点P从坐标原点O出发,先按照“平移量”{3,1 }平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图(1)中画出四边形OABC;
}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图(1)中画出四边形OABC;
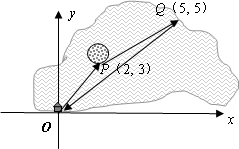
(3)如图(2),一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
 中画出四边形OABC.
中画出四边形OABC.科目:czsx 来源:2010年浙江省台州市初中毕业生学业考试数学试卷 题型:044
类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(-2)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图中画出四边形OABC

②证明四边形OABC是平行四边形
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O请用“平移量”加法算式表示它的航行过程.
科目:czsx 来源: 题型:
类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+(![]() )=1.
)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移![]() 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移![]() 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为![]() .
.
解决问题:
1.计算:{3,1}+{1,2};{1,2}+{3,1}.
2.①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
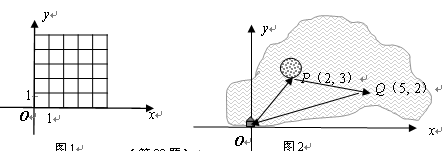
3.如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,2),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.

科目:czsx 来源: 题型:
类比学习:
一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+()=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
科目:czsx 来源: 题型:
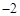 )=1.
)=1.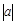 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移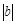 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为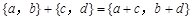 .
.
科目:czsx 来源: 题型:
 )=1.
)=1. 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 .
.