科目:czsx 来源:数学教研室 题型:044

科目:czsx 来源: 题型:解答题
 x+4与交换函数的图象的交点坐标;
x+4与交换函数的图象的交点坐标; x+b(b为常数)与交换函数的图象及纵轴所围三角形的面积为4,求b的值.
x+b(b为常数)与交换函数的图象及纵轴所围三角形的面积为4,求b的值.科目:czsx 来源:2012年浙江省绍兴市六所名校中考数学三模试卷(解析版) 题型:解答题
 x+4与交换函数的图象的交点坐标;
x+4与交换函数的图象的交点坐标;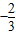 x+b(b为常数)与交换函数的图象及纵轴所围三角形的面积为4,求b的值.
x+b(b为常数)与交换函数的图象及纵轴所围三角形的面积为4,求b的值.科目:czsx 来源: 题型:
| a |
| x |
科目:czsx 来源: 题型:
| 2 |
| 3 |
| 2 |
| 3 |
科目:gzsx 来源: 题型:
| 3 |
科目:gzsx 来源:不详 题型:解答题
| 3 |
科目:gzsx 来源:虹口区二模 题型:解答题
| 3 |
科目:gzsx 来源:2013年浙江省温州市高一摇篮杯数学竞赛模拟试卷(二)(解析版) 题型:解答题
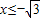 时,f(x)<g(x)恒成立.
时,f(x)<g(x)恒成立.科目:gzsx 来源:2008年上海市虹口区高考数学二模试卷(文理合卷)(解析版) 题型:解答题
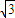 时,恒有f(x)<g(x)
时,恒有f(x)<g(x)科目:czsx 来源: 题型:
下面是一个二次函数y=ax![]() +bx+c的自变量x和函数y的对应值表:
+bx+c的自变量x和函数y的对应值表:
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | … |
根据表中提供的信息解答下列各题:
(1)求抛物线与y轴的交点坐标;
(2)抛物线的对称轴是在y轴的右边还是左边?并说明理由
(3)设抛物线与x轴两个交点分别为A、B,顶点为C,求△ABC的面积.
科目:czsx 来源: 题型:
科目:gzsx 来源: 题型:
| 3 |
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2010年湖北省黄冈中学高一新生入学数学试卷(解析版) 题型:解答题
科目:czsx 来源:2013届江苏省无锡市前洲中学九年级下学期期中考试数学试卷(带解析) 题型:解答题
阅读下列材料:
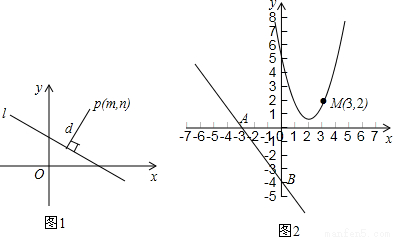
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+Bx+C=0(A、B、C是常数,且A、B不同时为0).如图1,点P(m,n)到直线l:Ax+Bx+C=0的距离(d)计算公式是:d=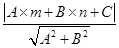 .
.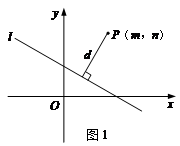
例:求点P(1,2)到直线y=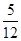 x-
x- 的距离d时,先将y=
的距离d时,先将y=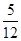 x-
x- 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d=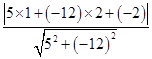 =
=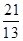 .
.
解答下列问题:
如图2,已知直线y=- x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).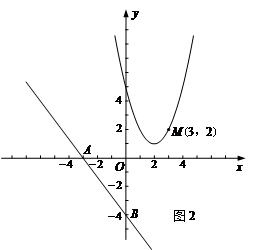
(1)求点M到直线AB的距离.
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
科目:czsx 来源:2012年湖南省郴州市中考数学试卷(解析版) 题型:解答题
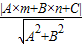 .
.
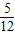 x-
x- 的距离d时,先将y=
的距离d时,先将y= 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d= =
= .
.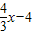 与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).科目:czsx 来源:2012-2013学年江苏省无锡市九年级下学期期中考试数学试卷(解析版) 题型:解答题
阅读下列材料:
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+Bx+C=0(A、B、C是常数,且A、B不同时为0).如图1,点P(m,n)到直线l:Ax+Bx+C=0的距离(d)计算公式是:d= .
.

例:求点P(1,2)到直线y=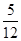 x-
x-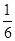 的距离d时,先将y=
的距离d时,先将y=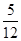 x-
x-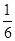 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d=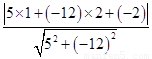 =
= .
.
解答下列问题:
如图2,已知直线y=-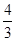 x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).

(1)求点M到直线AB的距离.
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
科目:czsx 来源:湖南省中考真题 题型:解答题
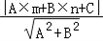 .
. 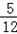 x﹣
x﹣ 的距离d时,先将y=
的距离d时,先将y=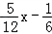 化为5x﹣12y﹣2=0,再由上述距离公式求得d=
化为5x﹣12y﹣2=0,再由上述距离公式求得d=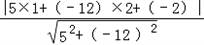 =
=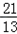 .
. 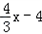 与x轴交于点A,与y轴交于点B,
与x轴交于点A,与y轴交于点B,