
科目:czsx 来源:2012-2013学年江西省景德镇市七年级下学期期中质量检测数学试卷(带解析) 题型:解答题
如图,已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,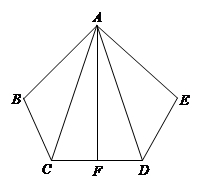
求证:(1)AC=AD;
(2)CF=DF.
科目:czsx 来源:2004年初中毕业升学考试(浙江温州卷)数学(带解析) 题型:解答题
如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.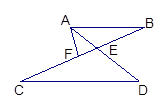
求证:(1) ∠EAF=∠B; (2)AF2=FE·FB
科目:czsx 来源:2015届江西省景德镇市七年级下学期期中质量检测数学试卷(解析版) 题型:解答题
如图,已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,
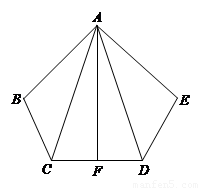
求证:(1)AC=AD;
(2)CF=DF.
科目:czsx 来源:2004年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:解答题
如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.
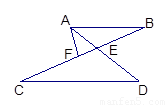
求证:(1) ∠EAF=∠B; (2)AF2=FE·FB
科目:czsx 来源: 题型:
 如图已知在⊙O中,直径AB=10,点E是OA上任意一点,过E作弦CD⊥AB,点F是弧BC上一点,连接AF交CE于H,连接AC、CF、BF.
如图已知在⊙O中,直径AB=10,点E是OA上任意一点,过E作弦CD⊥AB,点F是弧BC上一点,连接AF交CE于H,连接AC、CF、BF.科目:czsx 来源: 题型:

科目:czsx 来源:1+1轻巧夺冠·优化训练(冀教版)七年级数学(下) 冀教版银版 题型:022
已知:如图,AB∥CD,BC∥DE.
求证:∠B+∠D=180°.

证明:∵AB∥CD,
∴∠B=________(________).
∵BC∥________,
∴∠C+∠D=180°(________).
∴∠B+∠D=180°.
科目:czsx 来源:同步单元练习 八年级数学下 题型:044
已知如下图,AB∥CD,AD∥BC,求证∠A+∠BCE=![]() .
.

证明:因为AB∥CD(________),
所以∠A+∠D=________(________).
又因AD∥BC(________),
所以∠D=∠BCE(________).
所以∠A+∠BCE=![]() (________).
(________).