
科目:czsx 来源:贵州省六盘水市2012年中考数学试题 题型:022
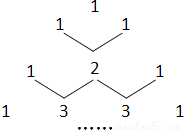
如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字;再如,(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式,(a+b)4=________.

科目:czsx 来源:2006年广州白云区初中毕业模拟考试数学试卷 题型:044
| |||||||||||||||
科目:czsx 来源: 题型:解答题
 x2+bx+c的图象与x轴交于A(-2,0),B(3,0)两点,点A关于正比例函数y=
x2+bx+c的图象与x轴交于A(-2,0),B(3,0)两点,点A关于正比例函数y= x的图象的对称点为C.
x的图象的对称点为C. x的图象于点D,连结AC,交正比例函数y=
x的图象于点D,连结AC,交正比例函数y= x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
科目:czsx 来源:2012年初中毕业升学考试(贵州六盘水卷)数学(带解析) 题型:填空题
如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数。
例如,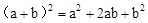 展开式中的系数1、2、1恰好对应图中第三行的数字;
展开式中的系数1、2、1恰好对应图中第三行的数字;
再如, 展开式中的系数1、3、3、1恰好对应图中第四行的数字。
展开式中的系数1、3、3、1恰好对应图中第四行的数字。
请认真观察此图,写出(a+b)4的展开式,(a+b)4= ▲ .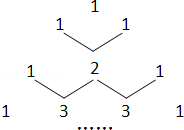
科目:czsx 来源:2013届江苏无锡市大桥区九年级上学期期末考试数学试卷(带解析) 题型:解答题
如图1,二次函数 的图象为抛物线,交x轴于A、B两点,交y轴于C点.其中AC=
的图象为抛物线,交x轴于A、B两点,交y轴于C点.其中AC= ,BC=
,BC= ,
, .
.
(1)求二次函数的解析式;
(2)若P点为抛物线上一动点且在x轴下方运动,当以P为圆心,1为半径的⊙P与直线BC相切时,求出符合条件的P点横坐标;
(3)如图2,若点E从点A出发,以每秒3个单位的速度沿着AB向点B匀速运动,点F从点A出发,以每秒 个单位的速度沿着AC向点C匀速运动.两点同时出发,当其中一点到达终点时,另一点也随之停止运动.过点E作AB的垂线
个单位的速度沿着AC向点C匀速运动.两点同时出发,当其中一点到达终点时,另一点也随之停止运动.过点E作AB的垂线 交抛物线于点E′,作点F关于直线
交抛物线于点E′,作点F关于直线 的对称点F′.设点E的运动时间为t(s),点F′ 能恰好在抛物线吗?若能,请直接写出t的值;若不能,请说明理由.
的对称点F′.设点E的运动时间为t(s),点F′ 能恰好在抛物线吗?若能,请直接写出t的值;若不能,请说明理由.

图1 图2
科目:czsx 来源:2013-2014学年浙江绍兴树人中学九年级第一学期期中学业评价数学试卷(解析版) 题型:解答题
如图,曲线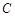 是函数
是函数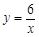 在第一象限内的图象,抛物线是函数
在第一象限内的图象,抛物线是函数 的图象.点
的图象.点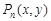 (
(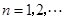 )在曲线
)在曲线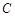 上,且
上,且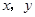 都是整数.
都是整数.
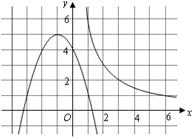
(1)求出所有的点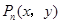 ;
;
(2)在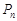 中任取两点作直线,求所有不同直线的条数;
中任取两点作直线,求所有不同直线的条数;
(3)从(2)的所有直线中任取一条直线,求所取直线与抛物线有公共点的概率.
科目:czsx 来源:2013年江苏省盐城市中考数学试卷(解析版) 题型:解答题
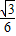 x2+bx+c的图象与x轴交于A(-2,0),B(3,0)两点,点A关于正比例函数y=
x2+bx+c的图象与x轴交于A(-2,0),B(3,0)两点,点A关于正比例函数y=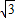 x的图象的对称点为C.
x的图象的对称点为C.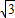 x的图象于点D,连结AC,交正比例函数y=
x的图象于点D,连结AC,交正比例函数y= x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.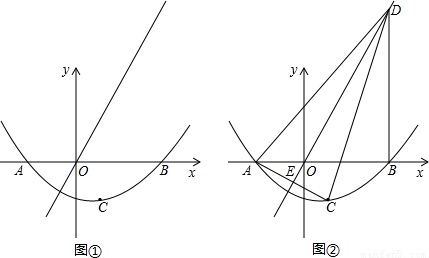
科目:czsx 来源:2013年初中毕业升学考试(江苏盐城卷)数学(解析版) 题型:解答题
如图①,若二次函数 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数 的图象的对称点为C。
的图象的对称点为C。
(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。

科目:czsx 来源:2012-2013学年江苏无锡市大桥区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图1,二次函数 的图象为抛物线,交x轴于A、B两点,交y轴于C点.其中AC=
的图象为抛物线,交x轴于A、B两点,交y轴于C点.其中AC= ,BC=
,BC=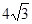 ,
, .
.
(1)求二次函数的解析式;
(2)若P点为抛物线上一动点且在x轴下方运动,当以P为圆心,1为半径的⊙P与直线BC相切时,求出符合条件的P点横坐标;
(3)如图2,若点E从点A出发,以每秒3个单位的速度沿着AB向点B匀速运动,点F从点A出发,以每秒 个单位的速度沿着AC向点C匀速运动.两点同时出发,当其中一点到达终点时,另一点也随之停止运动.过点E作AB的垂线
个单位的速度沿着AC向点C匀速运动.两点同时出发,当其中一点到达终点时,另一点也随之停止运动.过点E作AB的垂线 交抛物线于点E′,作点F关于直线
交抛物线于点E′,作点F关于直线 的对称点F′.设点E的运动时间为t(s),点F′ 能恰好在抛物线吗?若能,请直接写出t的值;若不能,请说明理由.
的对称点F′.设点E的运动时间为t(s),点F′ 能恰好在抛物线吗?若能,请直接写出t的值;若不能,请说明理由.


图1 图2
科目:czsx 来源:2012年初中毕业升学考试(贵州六盘水卷)数学(解析版) 题型:填空题
如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数。
例如, 展开式中的系数1、2、1恰好对应图中第三行的数字;
展开式中的系数1、2、1恰好对应图中第三行的数字;
再如, 展开式中的系数1、3、3、1恰好对应图中第四行的数字。
展开式中的系数1、3、3、1恰好对应图中第四行的数字。
请认真观察此图,写出(a+b)4的展开式,(a+b)4= ▲ .

科目:czsx 来源: 题型:解答题
如图,曲线 是函数
是函数 在第一象限内的图象,抛物线是函数
在第一象限内的图象,抛物线是函数 的图象.点
的图象.点 (
( )在曲线
)在曲线 上,且
上,且 都是整数.
都是整数.
(1)求出所有的点 ;
;
(2)在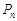 中任取两点作直线,求所有不同直线的条数;
中任取两点作直线,求所有不同直线的条数;
(3)从(2)的所有直线中任取一条直线,求所取直线与抛物线有公共点的概率.
科目:czsx 来源: 题型:解答题
如图①,若二次函数 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数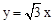 的图象的对称点为C。
的图象的对称点为C。
(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数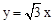 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数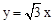 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。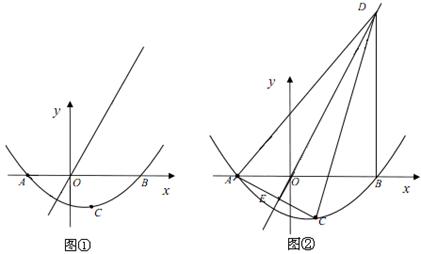
科目:czsx 来源:不详 题型:解答题
 是函数
是函数 在第一象限内的图象,抛物线是函数
在第一象限内的图象,抛物线是函数 的图象.点
的图象.点 (
( )在曲线
)在曲线 上,且
上,且 都是整数.
都是整数.
 ;
; 中任取两点作直线,求所有不同直线的条数;
中任取两点作直线,求所有不同直线的条数;科目:czsx 来源:不详 题型:解答题
 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数 的图象的对称点为C。
的图象的对称点为C。 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
科目:czsx 来源:不详 题型:解答题
| ||
| 6 |
| 3 |
| 3 |
| 3 |

科目:czsx 来源: 题型:填空题
 如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字;再如,(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式,(a+b)4=________.
如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字;再如,(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式,(a+b)4=________.科目:czsx 来源:2012年贵州省六盘水市中考数学试卷(解析版) 题型:填空题
科目:czsx 来源:2011年四川省绵阳市南山中学实验学校自主招生考试数学模拟试卷(一)(解析版) 题型:填空题
