练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知ab=5.求a

    已知ab=5.求a答案解析

    科目：czsx 来源：数学教研室 题型：022

    已知AB⊥CD,

    求证：∠1=∠2.

    　　证明：AB⊥CD(已知)

    　　　　  ∴∠1=90°,∠2=90°(　　　　　　　　 )

    　　　　  ∴∠1=∠2

    查看答案和解析>>

    科目：czsx 来源： 题型：022

    已知AB⊥CD,求证：∠1=∠2.

    证明：AB⊥CD(已知)

    ∴∠1=90°,∠2=90°(    )

    ∴∠1=∠2

    查看答案和解析>>

    科目：czsx 来源： 题型：013

    如图: 已知AB∥EF,

    求证: ∠BCF＝∠B+∠F,

    证明: 经过点C作CD∥AB

    　　∴∠B＝∠1(两直线平行, 内错角相等)

    　　∵AB∥EF(已知)CD∥AB(已作)

    　　∴CD∥EF(平行于同一条直线的两直线平行)

    　　∴∠F＝∠2(两直线平行, 内错角相等)

    　　∴∠1+∠2＝∠B+∠F(等式的性质)

    　　即∠BCF＝∠B+∠F(等量代换)

    证明中标注的理由

    [　　]

    A.全对　　B.部分对　　C.全错　　D.应有两线平行同位角相等

    　

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图，已知
    AB
    ，求作
    AB
    的中点M，找出
    AB
    所在圆的圆心．精英家教网

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知ab=1，试求分式：
    a
    a+1
    +
    b
    b+1
    的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知AB是半圆O的直径，AB=16，P点是AB上的一动点（不与A、B重合），PQ⊥AB，垂足为P，交半圆O于Q；PB是半圆O1的直径，⊙O2与半圆O、半圆O1及PQ都相切，切点分别为M、N、C．
    （1）当P点与O点重合时（如图1），求⊙O2的半径r；
    （2）当P点在AB上移动时（如图2），设PQ=x，⊙O2的半径r．求r与x的函数关系式，并求出r取值范围．精英家教网

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知AB=2，AD=4，∠DAB=90°，AD∥BC（如图），E是射线BC上的动点（点E与点B不重合），M是线段DE的中点．
    （1）设BE=x，△ABM的面积为y，求y关于x的函数解析式，并写出自变量的取值范围；
    （2）如果以线段AB为直径的圆与以线段DE为直径的圆外切，求线段BE的长；
    （3）连接BD，交线段AM于点N，如果以A，N，D为顶点的三角形与△BME相似，求线段BE的长．
    精英家教网

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知AB是半圆O的直径，点C在BA的延长线上运动（点C与点A不重合），以OC为直径的半圆M与半圆O交于点D，∠DCB的平分线与半圆M交于点E．
    精英家教网
    （1）求证：CD是半圆O的切线（图1）；
    （2）作EF⊥AB于点F（图2），猜想EF与已有的哪条线段的一半相等，并加以证明；
    （3）在上述条件下，过点E作CB的平行线交CD于点N，当NA与半圆O相切时（图3），求∠EOC的正切值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知AB与⊙O相切于点C，OA=OB，OA、OB与⊙O分别交于点D、E．
    （I）如图①，若⊙O的直径为8，AB=10，求OA的长（结果保留根号）；
    （II）如图②，连接CD、CE，若四边形ODCE为菱形，求
    ODOA
    的值．
    精英家教网

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知AB=10cm，直线AB上有一点C，BC=4cm，M是线段AC的中点，求AM的长．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C．精英家教网
    （1）如图①，若AB=2，∠P=30°，求AP的长（结果保留根号）；
    （2）如图②，若D为AP的中点，求证：直线CD是⊙O的切线．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知|ab-2|与（b-1）2互为相反数．
    （1）求a，b的值；
    （2）试求式子
    1
    ab
    +
    1
    (a+1)(b+1)
    +
    1
    (a+2)(b+2)
    +…+
    1
    (a+2006)(b+2006)
    值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

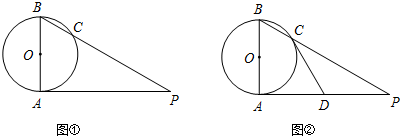
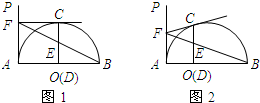    精英家教网已知AB为⊙O的直径，弦CD⊥AB，垂足为H．求证：AH•AB=AC2．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    精英家教网已知AB∥CD，AD、BC交于点O，已知AO=2，DO=4，CD=5，求AB的长．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知AB是⊙O的直径、弦CD⊥AB，垂足为E，弦AQ交CD于P，如果AB=10，CD=8，求：（1）DE的长；（2）AE的长；（3）AP•AQ的值．（要求：考生作图求解，图画在卷面右侧）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知
    ab
    a+b
    =4，
    ac
    a+c
    =5，
    bc
    b+c
    =6.    求17a+13b-7c的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知AB是半径为6的⊙O的直径，点C是⊙O的半径OA上的动点，PC⊥AB交⊙O于E，交OA于C，PC=10，PT是⊙O的切线（切点T在
    		BE
    上）．
    精英家教网
    （1）如图①当点C与点O重合时，求PT的长；
    （2）如图②当点C与点A重合时，求AT的长；
    （3）如图③设AC=x，PT=y，试求y关于x的函数关系式，并写出x、y的取值范围．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知ab＞0，试求
    |a|
    a
    +
    |b|
    b
    +
    |ab|
    ab
    的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知AB=2
    		3
    ，∠ABC=60°，D是线段AB上的动点，过D作DE⊥BC，垂足为E，四边形DEFG是正方形，点F在射线BC上，连接AG并延长交BC于点H．
    （1）求DE的取值范围；
    （2）当DE在什么范围取值时，△ABH为钝角三角形；
    （3）过B、A、G三点的圆与BC相交于点K，过K作这个圆的切线KL与DG的延长线相交于点L．若GL=1，这时点K与点F重合吗？请说明理由．
    精英家教网

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知AB是半圆O的直径，AP为过点A的半圆的切线，在
    AB
    上任取一点C（点C与A，B不重合），过精英家教网点C作CD⊥AB于D，E是CD的中点，连接BE并延长交AP于点F，连接CF．
    （1）当点C是
    AB
    的中点时（如图1），求证：直线CF是半圆O的切线；
    （2）当点C不是
    AB
    的中点时（如图2），试猜想直线CF与半圆O的位置关系，并证明你的猜想．

    查看答案和解析>>