练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >如图,直线直线l与○O分离.OA⊥l于点A

    如图,直线直线l与○O分离.OA⊥l于点A答案解析

    科目：czsx 来源： 题型：

    如图直线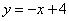与两坐标轴分别相交于A、B点，点M是线段AB上任意一点（A、B两点除外），过M分别作MC⊥OA于点C，MD⊥OB于D．

           （1）当点M在AB上运动时，你认为四边形OCMD的周长是否发生变化？并说明理由；

           （2）当点M运动到什么位置时，四边形OCMD的面积有最大值？最大值是多少？

    （3）当四边形OCMD为正方形时，将四边形OCMD沿着x轴的正方向移动，设平移的距离为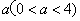，正方形OCMD与△AOB重叠部分的面积为S．试求S与的函数关系式并画出该函数的图象．

          

    查看答案和解析>>

    科目：czsx 来源：2015年初中毕业升学考试（河北卷）数学（解析版） 题型：解答题

    平面上，矩形ABCD与直径为QP的半圆K如图摆放，分别延长DA和QP交于点O，且∠BOQ＝60°，OQ＝OD＝3，OP＝2，OA＝AB＝1．让线段OD及矩形ABCD位置固定，将线段OQ连带着半圆K一起绕着点O按逆时针方向形如旋转，设旋转角为α（0°≤α≤60°）．

    发现（1）当α＝0°，即初始位置时，点P____直线AB上．（填“在”或“不在”）求当α是多少时，OQ经过点B？

    （2）在OQ旋转过程中．简要说明α是多少时，点P，A间的距离最小？并指出这个最小值：

    （3）如图，当点P恰好落在BC边上时．求α及S阴影．

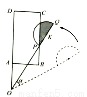
    拓展如图．当线段OQ与CB边交于点M，与BA边交于点N时，设BM＝x（x＞0），用含x的代数式表示BN的长，并求x的取值范围．

    探究当半圆K与矩形ABCD的边相切时，求sin α的值．

    查看答案和解析>>

    科目：czsx 来源：2016届江苏省无锡市锡北片九年级下期中数学试卷（解析版） 题型：解答题

    平面上，矩形ABCD与直径为QP的半圆K如图摆放，分别延长DA和QP交于点O，且∠DOQ＝60°，OQ＝OD＝3，OP＝2，OA＝AB＝1，让线段OD及矩形ABCD位置固定，将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转，设旋转角为α(0°≤α≤60°)．

    发现：

    （1）当α＝0°，即初始位置时，点P 直线AB上(选填“在”或“不在”)．

    当α= 时，OQ经过点B；

    （2）在OQ旋转过程中，α= 时，点P，A间的距离最小？PA最小值为 ；

    （3）探究当半圆K与矩形ABCD的边相切时，求sinα的值．

    查看答案和解析>>

    科目：czsx 来源：2016届江苏省无锡市锡山区东亭片九年级下期中数学试卷（解析版） 题型：填空题

    平面上，矩形ABCD与直径为QP的半圆K如图摆放，分别延长DA和QP交于点O，且∠DOQ＝60°，OQ＝OD＝3，OP＝2，OA＝AB＝1，让线段OD及矩形ABCD位置固定，将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转，设旋转角为α（0°≤α≤60°)．

    发现：

    （1）当α＝0°，即初始位置时，点P 直线AB上（选填“在”或“不在”)．当α= 时，OQ经过点B；

    （2）在OQ旋转过程中，α= 时，点P，A间的距离最小？PA最小值为 ；

    （3）探究当半圆K与矩形ABCD的边相切时，求sinα的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    16．平面上，矩形ABCD与直径为QP的半圆K如图摆放，分别延长DA和QP交于点O，且∠DOQ=60°，OQ=OD=3，OP=2，OA=AB=1，让线段OD及矩形ABCD位置固定，将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转，设旋转角为α（0°≤α≤60°）．
    发现：
    （1）当α=0°，即初始位置时，点P在直线AB上（选填“在”或“不在”）．
    当α=15°时，OQ经过点B；
    （2）在OQ旋转过程中，α=60°时，点P，A间的距离最小？PA最小值为1；
    （3）探究当半圆K与矩形ABCD的边相切时，求sin α的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

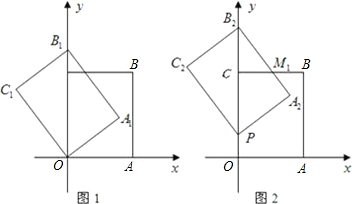
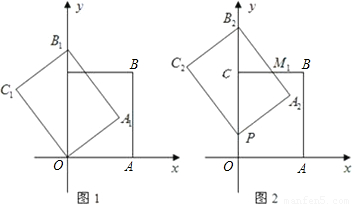
    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
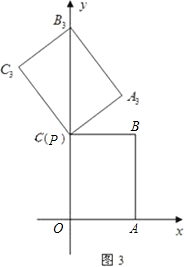
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．
    精英家教网精英家教网

    查看答案和解析>>

    科目：czsx 来源：鼓楼区2008年第一次模拟调研测试、九年级数学试卷 题型：044

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为(3，0)，C点的坐标为(0，4)．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC、A1B1相交于点M．

    (1)点B1的坐标为________，线段B1C的长为________；

    (2)将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．

    ①设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；

    ②是否存在一条直线l，如果将坐标纸沿直线l折叠，恰好使点A和B2重合，且点A2和B重合，若存在，请直接写出直线l的关系式；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

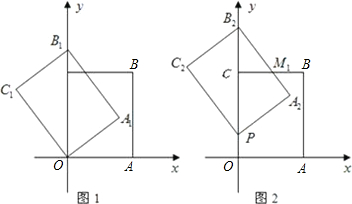
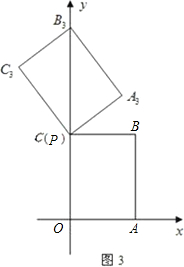
    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

    查看答案和解析>>

    科目：czsx 来源：第2章《二次函数》中考题集（43）：2.7 最大面积是多少（解析版） 题型：解答题

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

    查看答案和解析>>

    科目：czsx 来源：第25章《图形的变换》常考题集（12）：25.2 旋转变换（解析版） 题型：解答题

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

    查看答案和解析>>

    科目：czsx 来源：第25章《图形的变换》中考题集（14）：25.2 旋转变换（解析版） 题型：解答题

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

    查看答案和解析>>

    科目：czsx 来源：第34章《二次函数》常考题集（25）：34.4 二次函数的应用（解析版） 题型：解答题

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

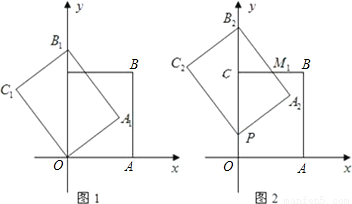
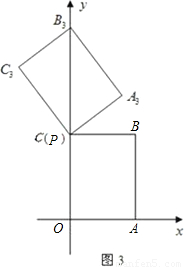
    查看答案和解析>>

    科目：czsx 来源：第34章《二次函数》中考题集（47）：34.4 二次函数的应用（解析版） 题型：解答题

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

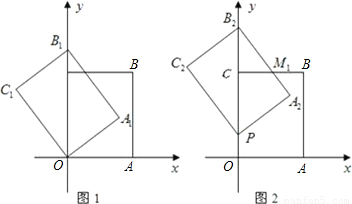
    查看答案和解析>>

    科目：czsx 来源：第2章《二次函数》常考题集（25）：2.3 二次函数的应用（解析版） 题型：解答题

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

    查看答案和解析>>

    科目：czsx 来源：第2章《二次函数》中考题集（46）：2.3 二次函数的应用（解析版） 题型：解答题

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

    查看答案和解析>>

    科目：czsx 来源：第6章《二次函数》常考题集（25）：6.4 二次函数的应用（解析版） 题型：解答题

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

    查看答案和解析>>

    科目：czsx 来源：第6章《二次函数》中考题集（47）：6.4 二次函数的应用（解析版） 题型：解答题

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

    查看答案和解析>>

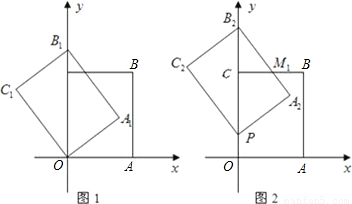
    科目：czsx 来源：第27章《二次函数》中考题集（46）：27.3 实践与探索（解析版） 题型：解答题

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

    查看答案和解析>>

    科目：czsx 来源：第26章《圆》常考题集（05）：26.1 旋转（解析版） 题型：解答题

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

    查看答案和解析>>

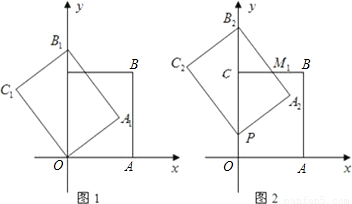
    科目：czsx 来源：第26章《圆》中考题集（06）：26.1 旋转（解析版） 题型：解答题

    如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
    （1）求点B1的坐标与线段B1C的长；
    （2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
    （3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．

    查看答案和解析>>