科目：gzsx 来源： 题型：

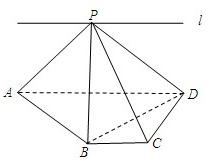
如图，ABCD为直角梯形，∠C=∠CDA=90°，AD=2BC=2CD，P为平面ABCD外一点，且PB⊥BD．
（1）求证：PA⊥BD；
（2）若PC与CD不垂直，求证：PA≠PD；
（3）若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD．

科目：gzsx 来源：2015届天津市高三上学期零月月考文科数学试卷（解析版） 题型：解答题

科目：gzsx 来源： 题型：解答题

科目：gzsx 来源：不详 题型：解答题

如图，ABCD为直角梯形，∠C=∠CDA=90°，AD=2BC=2CD，P为平面ABCD外一点，且PB⊥BD．
（1）求证：PA⊥BD；
（2）若PC与CD不垂直，求证：PA≠PD；
（3）若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD．

科目：gzsx 来源：2012-2013学年江苏省南通市通州区平潮高中高二（上）期中数学试卷（文科）（解析版） 题型：解答题

如图，ABCD为直角梯形，∠C=∠CDA=90°，AD=2BC=2CD，P为平面ABCD外一点，且PB⊥BD．
（1）求证：PA⊥BD；
（2）若PC与CD不垂直，求证：PA≠PD；
（3）若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD．

科目：gzsx 来源：2012-2013学年江苏省南通市通州区平潮高中高二（上）期中数学试卷（理科）（解析版） 题型：解答题

如图，ABCD为直角梯形，∠C=∠CDA=90°，AD=2BC=2CD，P为平面ABCD外一点，且PB⊥BD．
（1）求证：PA⊥BD；
（2）若PC与CD不垂直，求证：PA≠PD；
（3）若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD．

科目：gzsx 来源：2012-2013学年江苏省南通市通州区平潮高中高二（上）期中数学试卷（文科）（解析版） 题型：解答题

如图，ABCD为直角梯形，∠C=∠CDA=90°，AD=2BC=2CD，P为平面ABCD外一点，且PB⊥BD．
（1）求证：PA⊥BD；
（2）若PC与CD不垂直，求证：PA≠PD；
（3）若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD．

科目：gzsx 来源：2012-2013学年江苏省南通市通州区平潮高中高二（上）期中数学试卷（理科）（解析版） 题型：解答题

如图，ABCD为直角梯形，∠C=∠CDA=90°，AD=2BC=2CD，P为平面ABCD外一点，且PB⊥BD．
（1）求证：PA⊥BD；
（2）若PC与CD不垂直，求证：PA≠PD；
（3）若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD．

科目：gzsx 来源：《第1章 空间几何体》2010年单元测试卷（3）（解析版） 题型：解答题

如图，ABCD为直角梯形，∠C=∠CDA=90°，AD=2BC=2CD，P为平面ABCD外一点，且PB⊥BD．
（1）求证：PA⊥BD；
（2）若PC与CD不垂直，求证：PA≠PD；
（3）若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD．

科目：gzsx 来源：2009-2010学年江苏省南通市通州中学高三（上）期末数学试卷（解析版） 题型：解答题

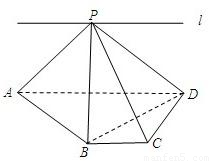
如图，ABCD为直角梯形，∠C=∠CDA=90°，AD=2BC=2CD，P为平面ABCD外一点，且PB⊥BD．
（1）求证：PA⊥BD；
（2）若PC与CD不垂直，求证：PA≠PD；
（3）若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD．

科目：gzsx 来源：2010年福建省高考数学一轮复习：14.3 平行关系（解析版） 题型：解答题

如图，ABCD为直角梯形，∠C=∠CDA=90°，AD=2BC=2CD，P为平面ABCD外一点，且PB⊥BD．
（1）求证：PA⊥BD；
（2）若PC与CD不垂直，求证：PA≠PD；
（3）若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD．

科目：gzsx 来源：2010年江苏省高三数学中等生强化练习（7）（解析版） 题型：解答题

如图，ABCD为直角梯形，∠C=∠CDA=90°，AD=2BC=2CD，P为平面ABCD外一点，且PB⊥BD．
（1）求证：PA⊥BD；
（2）若PC与CD不垂直，求证：PA≠PD；
（3）若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD．

科目：gzsx 来源：2010年高考数学小题限时训练试卷（12）（解析版） 题型：解答题

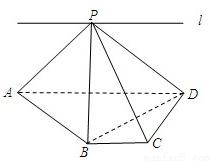
如图，ABCD为直角梯形，∠C=∠CDA=90°，AD=2BC=2CD，P为平面ABCD外一点，且PB⊥BD．
（1）求证：PA⊥BD；
（2）若PC与CD不垂直，求证：PA≠PD；
（3）若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD．

科目：gzsx 来源： 题型：

已知在四棱锥P-ABCD中，AD∥BC，AD⊥CD，PA=PD=AD=2BC=2CD，E，F分别是AD，PC的中点．
（Ⅰ）求证AD⊥平面PBE；
（Ⅱ）求证PA∥平面BEF；
（Ⅲ）若PB=AD，求二面角F-BE-C的大小．

科目：gzsx 来源： 题型：

已知在四棱锥P-ABCD中，AD∥BC，AD⊥CD，PA=PD=AD=2BC=2CD，E，F分别是AD，PC的中点．
（Ⅰ）求证AD⊥平面PBC；
（Ⅱ）若PB=AD，求二面角F-BE-C的大小．

科目：gzsx 来源： 题型：解答题

19．如图，四棱锥P-ABCD中，AD∥BC，AD⊥DC，AD=2BC=2CD=2，侧面APD为等腰直角三角形，PA⊥PD，平面PAD⊥平面ABCD．
（Ⅰ）求证：PA⊥面PCD；
（Ⅱ）求二面角A-PB-C的余弦值．

科目：gzsx 来源： 题型：

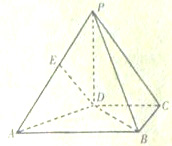
在四棱锥P-ABCD中，PD⊥底面ABCD，AB∥CD，AB⊥BC，AB=2BC=2CD，E是PA的中点．
（I）求证：DE∥平面PBC；
（II）求证：AD⊥PB．

科目：gzsx 来源：2012-2013学年山东省临沂市临沭县高三（上）期中数学试卷（文科）（解析版） 题型：解答题

在四棱锥P-ABCD中，PD⊥底面ABCD，AB∥CD，AB⊥BC，AB=2BC=2CD，E是PA的中点．
（I）求证：DE∥平面PBC；
（II）求证：AD⊥PB．

科目：gzsx 来源：2012-2013学年山东省临沂市高三（上）期中数学试卷（文科）（解析版） 题型：解答题

在四棱锥P-ABCD中，PD⊥底面ABCD，AB∥CD，AB⊥BC，AB=2BC=2CD，E是PA的中点．
（I）求证：DE∥平面PBC；
（II）求证：AD⊥PB．

科目：gzsx 来源：2012-2013学年山东省临沂市临沭县高三（上）期中数学试卷（文科）（解析版） 题型：解答题

在四棱锥P-ABCD中，PD⊥底面ABCD，AB∥CD，AB⊥BC，AB=2BC=2CD，E是PA的中点．
（I）求证：DE∥平面PBC；
（II）求证：AD⊥PB．