
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2015-2016学年山东省济宁市微山县七年级下期中数学试卷(解析版) 题型:解答题
在平面直角坐标系中,点A的坐标是(3a﹣5,a+1)
(1)若点A在y轴上,求a的值及点A的坐标.
(2)若点A到x轴的距离与到y轴的距离相等;求a的值及点A的坐标.
科目:czsx 来源: 题型:
2
| ||
| 3 |
| ||
| 3 |
4
| ||
| 3 |
| 2 |
| 2 |
 是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由. 科目:czsx 来源: 题型:
| 4 |
| x |
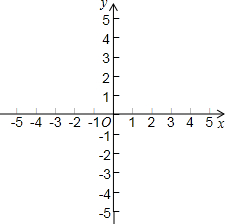 1交于点A(3,n).
1交于点A(3,n).| 4 |
| x |
科目:czsx 来源: 题型:044
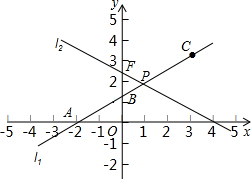
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0,![]() ),直线l2的函数表达式为
),直线l2的函数表达式为![]() ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
(1)
填空:直线l1的函数表达式是 ▲ ,交点P的坐标是 ▲ ,∠FPB的度数是 ▲ ;(2)
当⊙C和直线l2相切时,请证明点P到直线CM的距离等于⊙C的半径R,并写出R=(3)
当⊙C和直线l2不相离时,已知⊙C的半径R=
科目:czsx 来源:新课程 新理念 新思维·训练编·数学 九年级下册(苏教版) 苏教版 题型:059
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0,![]() ),直线l2的函数表达式为=-
),直线l2的函数表达式为=-![]() x+
x+![]() ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.

(1)填空:直线l1的函数表达式是________,交点P的坐标是________,∠FPB的度数是________;
(2)当⊙C和直线l2相切时,请证明点P到直线CM的距离等于⊙C的半径R,并写出R=![]() -2时a的值.
-2时a的值.
(3)当⊙C和直线l2不相离时,已知⊙C的半径R=![]() -2,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
-2,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
科目:czsx 来源:2006年浙江省初中毕业生学业考试数学试题 题型:059
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0,![]() ),直线l2的函数表达式为y=-
),直线l2的函数表达式为y=-![]() x+
x+![]() ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.

(1)填空:直线l1的函数表达式是________,交点P的坐标是________,∠FPB的度数是________;
(2)当⊙C和直线l2相切时,请证明点P到直线的距离CM等于⊙C的半径R,并写出R=![]() 时a的值.
时a的值.
(3)当⊙C和直线l2不相离时,已知⊙C的半径R=![]() ,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
科目:czsx 来源: 题型:解答题
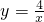 的图象与抛物线y=x2+(9m+4)x+m-
的图象与抛物线y=x2+(9m+4)x+m-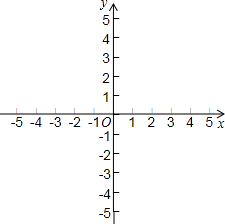 1交于点A(3,n).
1交于点A(3,n).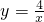 (x>0)的图象于点C,且AC=2AB,求B、C两点的坐标;
(x>0)的图象于点C,且AC=2AB,求B、C两点的坐标;科目:czsx 来源:2012届湖北省蕲春县刘河中学九年级上学期期中考试数学卷(B) 题型:解答题
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0, ),直线l2的函数表达式为
),直线l2的函数表达式为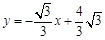 ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
【小题1】求直线l1的函数表达式;
【小题2】 当⊙C和直线l2相切时,请证明点P到直线CM的距离等于⊙C的半径R,并写出R= 时a的值.
时a的值.
【小题3】当⊙C和直线l2不相离时,已知⊙C的 半径R=
半径R= ,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.

科目:czsx 来源:2010-2011学年北京市门头沟区九年级(上)期末数学试卷(解析版) 题型:解答题
 的图象与抛物线y=x2+(9m+4)x+m-1交于点A(3,n).
的图象与抛物线y=x2+(9m+4)x+m-1交于点A(3,n).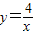 (x>0)的图象于点C,且AC=2AB,求B、C两点的坐标;
(x>0)的图象于点C,且AC=2AB,求B、C两点的坐标;
科目:czsx 来源:2011-2012学年湖北省九年级上学期期中考试数学卷(B) 题型:解答题
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0,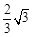 ),直线l2的函数表达式为
),直线l2的函数表达式为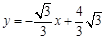 ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
1.求直线l1的函数表达式;
2. 当⊙C和直线l2相切时,请证明点P到直线CM的距离等于⊙C的半径R,并写出R=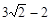 时a的值.
时a的值.
3.当⊙C和直线l2不相离时,已知⊙C的半径R=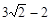 ,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.

科目:gzsx 来源:闸北区二模 题型:解答题
| ||
| 2 |
| 1 |
| 2 |
| 3 |
科目:czsx 来源:不详 题型:解答题
 ),直线l2的函数表达式为
),直线l2的函数表达式为 ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M. 时a的值.
时a的值. 半径R=
半径R= ,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.

科目:czsx 来源: 题型:
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0,![]() ),直线l2的函数表达式为
),直线l2的函数表达式为![]() ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
1.求直线l1的函数表达式;
2. 当⊙C和直线l2相切时,请证明点P到直线CM的距离等于⊙C的半径R,并写出R=![]() 时a的值.
时a的值.
3.当⊙C和直线l2不相离时,已知⊙C的半径R=![]() ,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
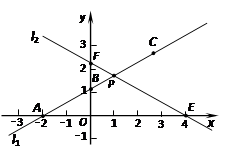
科目:gzsx 来源: 题型:
| ||
| 2 |
| 1 |
| 2 |
| 3 |
科目:czsx 来源:不详 题型:解答题
 时,
时, ,2)中可以成为正方形ABCD的“等距圆”的圆心的是_______________;
,2)中可以成为正方形ABCD的“等距圆”的圆心的是_______________;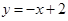 上,且⊙P是正方形ABCD的“等距圆”,则点P的坐标为_______________;
上,且⊙P是正方形ABCD的“等距圆”,则点P的坐标为_______________;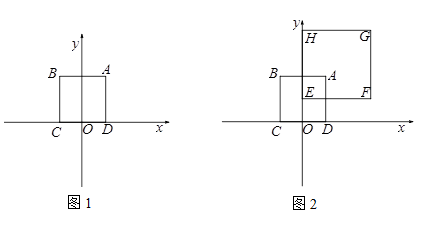
科目:czsx 来源:2014年北京市海淀区中考二模数学试卷(解析版) 题型:解答题
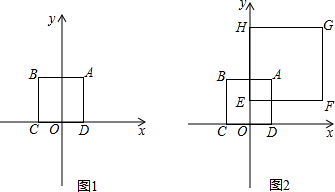
对于半径为r的⊙P及一个正方形给出如下定义:若⊙P上存在到此正方形四条边距离都相等的点,则称⊙P是该正方形的“等距圆”.如图1,在平面直角坐标系xOy中,正方形ABCD的顶点A的坐标为(2,4),顶点C、D在x轴上,且点C在点D的左侧.
(1)当r= 时,
时,
①在P1(0,-3),P2(4,6),P3(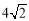 ,2)中可以成为正方形ABCD的“等距圆”的圆心的是_______________;
,2)中可以成为正方形ABCD的“等距圆”的圆心的是_______________;
②若点P在直线 上,且⊙P是正方形ABCD的“等距圆”,则点P的坐标为_______________;
上,且⊙P是正方形ABCD的“等距圆”,则点P的坐标为_______________;
(2)如图2,在正方形ABCD所在平面直角坐标系xOy中,正方形EFGH的顶点F的坐标为(6,2),顶点E、H在y轴上,且点H在点E的上方.
①若⊙P同时为上述两个正方形的“等距圆”,且与BC所在直线相切,求⊙P 在y轴上截得的弦长;
②将正方形ABCD绕着点D旋转一周,在旋转的过程中,线段HF上没有一个点能成为它的“等距圆”的圆心,则r的取值范围是_______________.

科目:czsx 来源: 题型:
| 2 |
| 2 |
科目:czsx 来源: 题型:
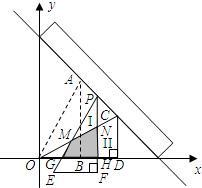 从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至△PEF处时,设PE,PF与OC分别交于点M,N,与x轴分别交于点G,H.
从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至△PEF处时,设PE,PF与OC分别交于点M,N,与x轴分别交于点G,H.科目:czsx 来源:浙江省杭州市青春中学2012届九年级中考模拟数学试题 题型:044
如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的△AOB,△COD处,直角边OB,OD在x轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至△PEF处时,设PE.PF与OC分别交于点M,N,与x轴分别交于点G,H.
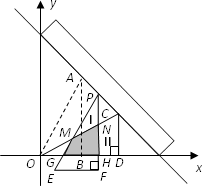
(1)求直线AC所对应的函数关系式;
(2)当点P是线段AC(端点除外)上的动点时,试探究:
①点M到x轴的距离h与线段BH的长是否总相等?请说明理由;
②两块纸板重叠部分(图中的阴影部分)的面积S是否存在最大值?若存在,求出这个最大值及S取最大值时点P的坐标;若不存在,请说明理由.