
科目:czsx 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期期末考试数学试卷(解析版) 题型:解答题
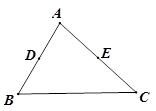
(12分)如图所示,E是正方形ABCD的边AB上的动点,正方形的边长为4, EF⊥DE交BC于点F.


(1)求证:△ADE ∽△BEF ;
(2)AE=x,BF=y.当x取什么值时,y有最大值? 并求出这个最大值;
(3)已知D、C 、F、E四点在同一个圆上,连接CE、DF,若sin∠CEF =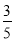 ,求此圆直径.
,求此圆直径.
科目:gzwl 来源: 题型:解答题

科目:czsx 来源: 题型:
| 10 |
| 10 |
科目:czsx 来源: 题型:
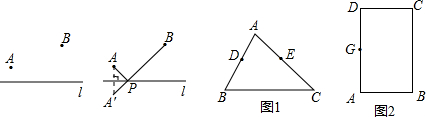
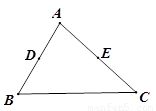
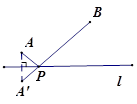
小明在学习轴对称的时候,老师留了这样一道思考题:如图,已知在直线l的同侧有A、B两点,请你在直线l上确定一点P,使得PA+PB的值最小.小明通过独立思考,很快得出了解决这个问题的正确方法,他的作法是这样的:

①作点A关于直线l的对称点A′.
②连结A′B,交直线l于点P.
则点P为所求.

请你参考小明的作法解决下列问题:
(1)如图,在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使得△PDE的周长最小.
①在图1中作出点P.(三角板、刻度尺作图,保留作图
痕迹,不写作法)
②请直接写出△PDE周长的最小值 .
(2)如图在矩形ABCD中,AB=4,BC=6,G为边AD的中点,若E、F为边AB上的两个动点,点E在点F左侧,且EF=1,当四边形CGEF的周长最小时,请你在图2中确定点E、F的位置.(三角板、刻度尺作图,保留作图痕迹,不写作法),并直接写出四边形CGEF周长的最小值 .

科目:czsx 来源: 题型:
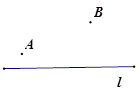


科目:czsx 来源:2012届北京市通州区九年级中考一模数学卷(带解析) 题型:解答题
小明在学习轴对称的时候,老师留了这样一道思考题:如图,已知在直线l的同侧有A、B两点,请你在直线l上确定一点P,使得PA+PB的值最小.小明通过独立思考,很快得出了解决这个问题的正确方法,他的作法是这样的: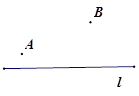
①作点A关于直线l的对称点A′.
②连结A′B,交直线l于点P.
则点P为所求.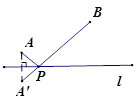
请你参考小明的作法解决下列问题:
(1)如图,在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使得△PDE的周长最小.
①在图1中作出点P.(三角板、刻度尺作图,保留作图
痕迹,不写作法)
②请直接写出△PDE周长的最小值 .
(2)如图在矩形ABCD中,AB=4,BC=6,G为边AD的中点,若E、F为边AB上的两个动点,点E在点F左侧,且EF=1,当四边形CGEF的周长最小时,请你在图2中确定点E、F的位置.(三角板、刻度尺作图,保留作图痕迹,不写作法),并直接写出四边形CGEF周长的最小值 . 
科目:czsx 来源:2011-2012学年北京市通州区九年级中考一模数学卷(解析版) 题型:解答题
小明在学习轴对称的时候,老师留了这样一道思考题:如图,已知在直线l的同侧有A、B两点,请你在直线l上确定一点P,使得PA+PB的值最小.小明通过独立思考,很快得出了解决这个问题的正确方法,他的作法是这样的:

①作点A关于直线l的对称点A′.
②连结A′B,交直线l于点P.
则点P为所求.
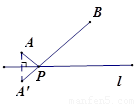
请你参考小明的作法解决下列问题:
(1)如图,在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使得△PDE的周长最小.
①在图1中作出点P.(三角板、刻度尺作图,保留作图
痕迹,不写作法)
②请直接写出△PDE周长的最小值 .
(2)如图在矩形ABCD中,AB=4,BC=6,G为边AD的中点,若E、F为边AB上的两个动点,点E在点F左侧,且EF=1,当四边形CGEF的周长最小时,请你在图2中确定点E、F的位置.(三角板、刻度尺作图,保留作图痕迹,不写作法),并直接写出四边形CGEF周长的最小值 .

科目:czsx 来源:不详 题型:解答题



科目:czsx 来源: 题型:解答题
科目:czsx 来源:2012年北京市通州区中考数学一模试卷(解析版) 题型:解答题
科目:czsx 来源: 题型:
小明在学习轴对称的时候,老师留了这样一道思考题 :如图,已知在直线l的同侧有A、B两点,请你在直线l上确定一点P,使得PA+PB的值最小.小明通过独立思考,很快得出了
:如图,已知在直线l的同侧有A、B两点,请你在直线l上确定一点P,使得PA+PB的值最小.小明通过独立思考,很快得出了 解决这个问题的正确方法,他的作法是这样的:
解决这个问题的正确方法,他的作法是这样的:
①作点A关于直线l的对称点A′.②连结A′B,交直线l于点P.则点P为所求.
请你参考小明的作法解决下列问题:
(1)如图1,在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使得△PDE的周长最小.
①在图1中画出点P.(三角板、刻度尺画图,保留画图痕迹, 不写画法)
不写画法)
②请直接写出△PDE周长的最小值 .

 (2)如图2在矩形ABCD中,AB=4,BC=6,G为边AD的中点,若E、F为边AB上的两个动点,点E在点F左侧,且EF=1,当四边形CGEF的周长最小时,请你在图2中确定点E、F的位置.(三角板、刻度尺画图,保留画图痕迹,不写画法),并直接写出四边形CGEF周长的最小值 .
(2)如图2在矩形ABCD中,AB=4,BC=6,G为边AD的中点,若E、F为边AB上的两个动点,点E在点F左侧,且EF=1,当四边形CGEF的周长最小时,请你在图2中确定点E、F的位置.(三角板、刻度尺画图,保留画图痕迹,不写画法),并直接写出四边形CGEF周长的最小值 .
 |

科目:czsx 来源: 题型:
| EG |
| FH |
| b |
| a |
| EG |
| FH |
| b |
| a |
科目:czsx 来源: 题型:
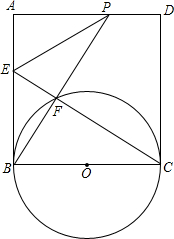 交⊙O于点F,CF的延长线交AB于点E,连接PE.
交⊙O于点F,CF的延长线交AB于点E,连接PE.科目:czsx 来源:2013年江苏省徐州市高级中等学校招生考试数学 题型:044
如图,二次函数y=![]() x2+bx-
x2+bx-![]() 的图象与x轴交于点A(-3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(-3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
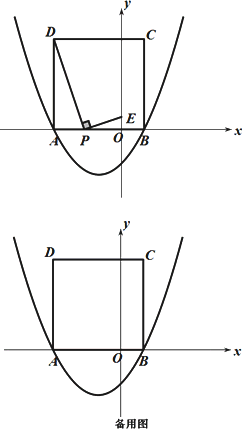
(1)请直接写出点D的坐标:________;
(2)当点P在线段AO(点P不与A,O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
科目:czsx 来源: 题型:解答题
 x2+bx-
x2+bx- 的图象与x轴交于点A(-3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(-3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
科目:czsx 来源: 题型:解答题
 点,AB所在直线为x轴建立平面直角坐标系.
点,AB所在直线为x轴建立平面直角坐标系.科目:czsx 来源: 题型:解答题
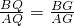 ,是否成立,并就你的判断加以说明.
,是否成立,并就你的判断加以说明.
科目:czsx 来源: 题型:
如图,正方形ABCD的边长为4.点E在边AB上,且AE=1.点F为边CD上一动点,且DF=m.以A为原点,AB所在直线为x轴建立平面直角坐标系.
(1)连接EF,求四边形AEFD的面积s关于m的函数关系式;
(2)若直线EF将正方形ABCD分成面积相等的两部分.求此时直线EF对应的函数关系式;
(3)在正方形ABCD的边上是否存在点P,使△PCE是等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.(本题9分)

科目:czsx 来源: 题型:
如图,二次函数y=x2+bx﹣的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)请直接写出点D的坐标: (﹣3,4) ;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
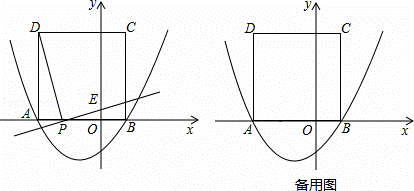
科目:czsx 来源:2013-2014学年江苏省无锡市惠山北片九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,二次函数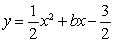 的图象与x轴交于点A(-3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(-3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.

(1)请直接写出点D的坐标:
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.