
科目:czsx 来源:2013-2014学年中考数学章节复习测试全等三角形练习卷(解析版) 题型:解答题
如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC中点.

(1)写出O点到△ABC三个顶点A、B、C的距离关系(不要求证明);
(2)如果M、N分别在线段AB、AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,并证明你的结论.
科目:czsx 来源:不详 题型:解答题

科目:czsx 来源: 题型:
如图8-15,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC中点.

图8-15
(1)写出O点到△ABC三个顶点A、B、C的距离关系(不要求证明);
(2)如果M、N分别在线段AB、AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,并证明你的结论.
科目:czsx 来源: 题型:
如图8-15,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC中点.

图8-15
(1)写出O点到△ABC三个顶点A、B、C的距离关系(不要求证明);
(2)如果M、N分别在线段AB、AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,并证明你的结论.
科目:czsx 来源: 题型:单选题
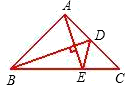 如图Rt△ABC中,∠BAC=90°,AB=AC,D为AC的中点,AE⊥BD交BC于E,若∠BDE=a,∠ADB的大小是
如图Rt△ABC中,∠BAC=90°,AB=AC,D为AC的中点,AE⊥BD交BC于E,若∠BDE=a,∠ADB的大小是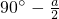
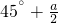
科目:czsx 来源: 题型:
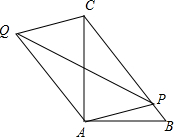 如图Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为
如图Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为科目:czsx 来源: 题型:
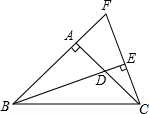 如图,△ABC中,∠BAC=90°,AB=AC,BD是∠ABC的平分线,BD的延长线垂直过C点的直线于E,直线CE交BA的延长线于F.求证:
如图,△ABC中,∠BAC=90°,AB=AC,BD是∠ABC的平分线,BD的延长线垂直过C点的直线于E,直线CE交BA的延长线于F.求证:科目:czsx 来源:2016届河南中考数学押题试卷数学试卷(解析版) 题型:解答题
已知Rt△ABC,AB=AC,∠BAC=90°,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作Rt△ADE,AD=AE,连接CE.
(1)发现问题
如图①,当点D在边BC上时,
①请写出BD和CE之间的数量关系为________,位置关系为________;
②线段CE+CD=________AC;
(2)尝试探究
如图②,当点D在边BC的延长线上且其他条件不变时,(1)中AC、CE、CD之间存在的数量关系是否成立?若成立,请证明;若不成立,请说明理由;
(3)拓展延伸
如图③,当点D在边CB的延长线上且其他条件不变时,若BC=4,CE=2,求线段CD的长.

科目:czsx 来源: 题型:
 如图,在Rt△ABC中,AC=2AB,∠BAC=90°,D是AC的中点,在Rt△DEA中,∠AED=90°,∠EAD=45°,连结BE、CE,试猜想BE和EC的关系,并证明你的猜想.
如图,在Rt△ABC中,AC=2AB,∠BAC=90°,D是AC的中点,在Rt△DEA中,∠AED=90°,∠EAD=45°,连结BE、CE,试猜想BE和EC的关系,并证明你的猜想.| 1 |
| 2 |
|
| 1 |
| 2 |
|
科目:czsx 来源: 题型:
如图,在RtΔABC中,AC=BC,∠ACB=90°,AD平分∠BAC,
BE AD交AC的延长线于F,E为垂足.则结论:(1)AD=BF;
AD交AC的延长线于F,E为垂足.则结论:(1)AD=BF;
(2)CF=CD;(3)AC+CD=AB;(4)BE=CF;(5)BF=2BE,其
中正确的结论个数是( ).
A.2 B.3 C.4 D.5

科目:czsx 来源: 题型:解答题

科目:czsx 来源:2014人教版八年级上册(专题训练 状元笔记)数学:第12章全等三角形 题型:044
如图,在Rt△ABC中,∠C=90°,∠BAC∶∠B=2∶1,AD是∠BAC的角平分线,DE⊥AB于点E,AC=3 cm,求BE的长.

科目:czsx 来源:1+1轻巧夺冠·优化训练(北京课改版)八年级数学(下) 北京课改版 题型:047
如图,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC交BC于D.
求证:AB=AC+CD.

科目:czsx 来源:学习周报 数学 北师大九年级版 2009-2010学年 第3期 总第159期 北师大版 题型:013
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线交AB于点D,交BC于点E,AE平分∠BAC,那么下列关系式中不成立的是

∠B=∠CAE
∠DEA=∠CEA
∠B=∠BAE
AC=2EC
科目:czsx 来源:学习周报 数学 沪科九年级版 2009-2010学年 第19期 总第175期 沪科版 题型:047
如图,在
Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上一点,DE=DC,以点D为圆心,DB的长为半径画圆.
求证:
(1)AC是⊙D的切线;(2)AB+EB=AC.
科目:czsx 来源:2009年云南省高中(中专)招生统一考试数学试题 题型:022
如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线AD交BC于点D,DE∥AC,DE交AB于点E,M为BE的中点,连结DM.在不添加任何辅助线和字母的情况下,图中的等腰三角形是________.(写出一个即可)

科目:czsx 来源:2010年四川省内江市高中阶段教育学校招生考试数学试卷 题型:044
如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC相切于点D.
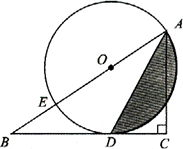
(1)求证:AD平分∠BAC.
(2)若AC=3,AE=4.
①求AD的值;②求图中阴影部分的面积.
科目:czsx 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是∠BAC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
 (1)求证:AC=AE;
(1)求证:AC=AE;
(2)求△ACD外接圆的直径.
科目:czsx 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是∠BAC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
 (1)求证:AC=AE;
(1)求证:AC=AE;
(2)求△ACD外接圆的直径.