科目:czsx 来源:学习周报 数学 沪科八年级版 2009-2010学年 第19~26期 总175~182期 沪科版 题型:022
三角形的分类:
(1)按边长关系,可分为:
(2)按角的大小,可分为:

科目:czsx 来源:1+1轻巧夺冠·优化训练 数学 七年级下 (华东师大版) 银版 华东师大版 题型:022
三角形的一个外角小于90°,此三角形按角分类应为________三角形.
科目:czsx 来源:学习周报 数学 沪科八年级版 2009-2010学年 第8期 总164期 沪科版 题型:022
如果三角形的三个内角度数之比为1∶1∶2,则这个三角形的形状是________(按角分类).
科目:czsx 来源:黄冈难点课课练 七年级数学下册(华师大版) 题型:022
一个三角形的两个角分别为![]() ,
,![]() ,若按边分类,它是________三角形;若按角分类是________三角形.
,若按边分类,它是________三角形;若按角分类是________三角形.
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:单选题

科目:czsx 来源:北京同步题 题型:填空题
科目:czsx 来源: 题型:
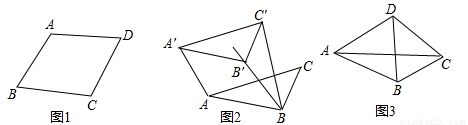
类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”。
(1)概念理解
如图1,在四边形ABCD中,添加一个条件,使得四边形ABCD是“等邻边四边形”,请写出你添加的一个条件;2-1-c-n-j-y
(2)问题探究
①小红猜想:对角线互相平分的“等邻边四边形”是菱形,她的猜想正确吗?请说明理由;
②如图2,小红画了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将Rt△ABC沿∠B的平分线BB’方向平移得到△A’B’C’,连结AA’,BC’。小红要使平移后的四边形ABC’A’是“等邻边四边形”,应平移多少距离(即线段BB’的长)?
(3)应用拓展
如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,AC= AB。试探究BC,CD,BD的数量关系。
AB。试探究BC,CD,BD的数量关系。

科目:czsx 来源: 题型:
类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念理解
如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)问题探究
①小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由。
②如图2,小红画了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将Rt△ABC沿
∠ABC的平分线BB'方向平移得到△A'B'C',连结AA',BC'.小红要是平移后的四边形ABC'A'是“等邻边四边形”,应平移多少距离(即线段BB'的长)?
(3)应用拓展
如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD==90°,AC,BD为对角线,AC= AB.试探究BC,CD,BD的数量关系.
AB.试探究BC,CD,BD的数量关系.

科目:czsx 来源:2015年初中毕业升学考试(浙江嘉兴卷)数学(解析版) 题型:解答题
类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念理解
如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)问题探究
①小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由。
②如图2,小红画了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将Rt△ABC沿∠ABC的平分线BB'方向平移得到△A'B'C',连结AA',BC'.小红要是平移后的四边形ABC'A'是“等邻边四边形”,应平移多少距离(即线段BB'的长)?
(3)应用拓展
如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD==90°,AC,BD为对角线,AC=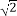 AB.试探究BC,CD,BD的数量关系.
AB.试探究BC,CD,BD的数量关系.
科目:czsx 来源: 题型:
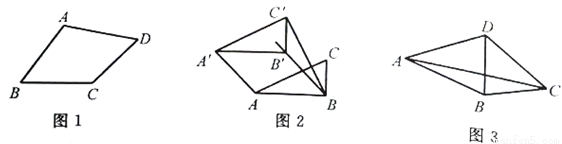
类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由.
(3)如图2,小红作了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.小红要使得平移后的四边形ABC′A′是“等邻边四边形”,应平移多少距离(即线段B′B的长)?


科目:czsx 来源:2016届福建省泉州市泉港区九年级上学期期中教学质量检测数学试卷(解析版) 题型:解答题
类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1) 概念理【解析】
如图1,在四边形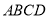 中,添加一个条件,使得四边形
中,添加一个条件,使得四边形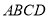 是“等邻边四边形”,请写出你添加的一个条件: .
是“等邻边四边形”,请写出你添加的一个条件: .
(2) 问题探究:
如图2,小红画了一个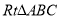 ,其中
,其中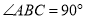 ,
,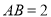 ,
, ,并将
,并将 沿
沿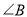 的平分线
的平分线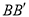 方向平移得到
方向平移得到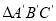 ,连结
,连结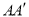 、
、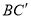 .小红要使平移后的四边形
.小红要使平移后的四边形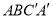 是“等邻边四边形”,应平移多少距离(即线段
是“等邻边四边形”,应平移多少距离(即线段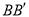 的长)?
的长)?
(3) 应用拓展:
如图3,“等邻边四边形”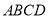 中,
中,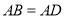 ,
,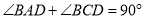 ,
, 、
、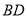 为对角线,
为对角线,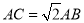 .试探究
.试探究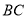 、
、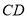 、
、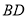 的数量关系.
的数量关系.