科目:czsx
来源:
题型:
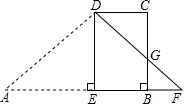
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-
,
)].
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30. 作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax2+bx+c图象的顶点坐标为(- ,
, )].
)].
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(17):2.6 何时获得最大利润(解析版)
题型:解答题
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-

,
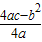
)].

查看答案和解析>>
科目:czsx
来源:第25章《图形的变换》中考题集(30):25.3 轴对称变换(解析版)
题型:解答题
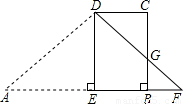
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-

,

)].
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(13):2.2 二次函数的图象与性质(解析版)
题型:解答题
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-

,

)].

查看答案和解析>>
科目:czsx
来源:第27章《二次函数》中考题集(13):27.2 二次函数的图象与性质(解析版)
题型:解答题
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-
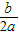
,

)].

查看答案和解析>>
科目:czsx
来源:第26章《二次函数》中考题集(12):26.1 二次函数(解析版)
题型:解答题
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-
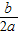
,

)].

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(13):2.4 二次函数y=ax2+bx+c的图象和性质(解析版)
题型:解答题
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-

,

)].

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(13):2.3 二次函数的性质(解析版)
题型:解答题
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-
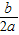
,
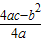
)].

查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(12):23.3. 二次函数y=ax2+bx+c的图象和性质(解析版)
题型:解答题
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-

,

)].

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,梯形ABCD中,AB
∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-
,
)].

查看答案和解析>>
科目:czsx
来源:
题型:
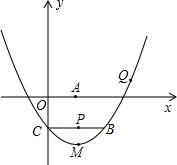
如图,过点C(0,-2)的抛物线y=ax
2+bx+c的顶点M坐标为(2,-3),过点C作CB∥x轴交抛物线于点B,点P在线段BC上,CP=m.
(1)求B点坐标,并用含m的代数式表示PB的长;
(2)点A,Q分别为x轴和抛物线上的动点,若恰好存在以CP为边,点A,C,P,Q为顶点的平行四边形,求出所有符合条件的点Q坐标;
(3)是否存在m值,使△MBP为等腰三角形?若存在,求出所有符合条件的m值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2010年全国中考数学试题汇编《图形的对称》(04)(解析版)
题型:解答题
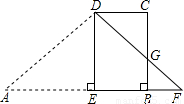
(2010•长春)如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-

,
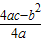
)].
查看答案和解析>>
科目:czsx
来源:2010年全国中考数学试题汇编《四边形》(07)(解析版)
题型:解答题
(2010•长春)如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-
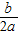
,
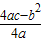
)].

查看答案和解析>>
科目:czsx
来源:2010年全国中考数学试题汇编《二次函数》(05)(解析版)
题型:解答题
(2010•长春)如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-

,

)].

查看答案和解析>>
科目:czsx
来源:2010年吉林省长春市中考数学试卷(解析版)
题型:解答题
(2010•长春)如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax
2+bx+c图象的顶点坐标为(-

,

)].

查看答案和解析>>
科目:czsx
来源:
题型:

已知二次函数y=ax
2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,若点A的坐标是(1,0),点B在点A的右侧.
(1)c=
;b=
(用含a的代数式表示);
(2)求a的取值范围;
(3)若过点C且平行于x轴的直线交该抛物线于另一点D,AD、BC交于点P,记△PCD的面积为S
1,△PAB的面积为S
2,求S
1-S
2的值.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图:直线y=-
如图:直线y=- x+4m(常数m>0)交x轴于A点、交y轴于B点,四边形AOBC是以OA、OB为边的梯形,OA∥BC.将梯形AOBC逆时针旋转90°到A1OB1C1,连接B1C交y轴于D.(如图)
x+4m(常数m>0)交x轴于A点、交y轴于B点,四边形AOBC是以OA、OB为边的梯形,OA∥BC.将梯形AOBC逆时针旋转90°到A1OB1C1,连接B1C交y轴于D.(如图)
(1)请指出A1、B1的坐标.(用含m的代数式表示)
(2)当A1DB1C1为平行四边形时,求C点的坐标.(用含m的代数式表示)
(3)若抛物线y=ax2+bx+c在(2)的条件下过A、B、C三点且与线段B1C另一交点为E,连接A1E,求:S△A1DE:S四边形AOBC的值.
查看答案和解析>>
科目:czsx
来源:2012年湖北省宜昌市中考适应性训练数学试卷(五)(解析版)
题型:解答题
如图:直线y=-

x+4m(常数m>0)交x轴于A点、交y轴于B点,四边形AOBC是以OA、OB为边的梯形,OA∥BC.将梯形AOBC逆时针旋转90°到A
1OB
1C
1,连接B
1C交y轴于D.(如图)
(1)请指出A
1、B
1的坐标.(用含m的代数式表示)
(2)当A
1DB
1C
1为平行四边形时,求C点的坐标.(用含m的代数式表示)
(3)若抛物线y=ax
2+bx+c在(2)的条件下过A、B、C三点且与线段B
1C另一交点为E,连接A
1E,求:S
△A1DE:S
四边形AOBC的值.

查看答案和解析>>
科目:czsx
来源:
题型:
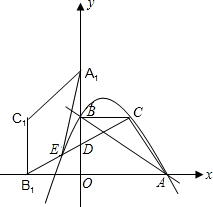
如图:直线y=-
x+4m(常数m>0)交x轴于A点、交y轴于B点,四边形AOBC是以OA、OB为边的梯形,OA∥BC.将梯形AOBC逆时针旋转90°到A
1OB
1C
1,连接B
1C交y轴于D.(如图)
(1)请指出A
1、B
1的坐标.(用含m的代数式表示)
(2)当A
1DB
1C
1为平行四边形时,求C点的坐标.(用含m的代数式表示)
(3)若抛物线y=ax
2+bx+c在(2)的条件下过A、B、C三点且与线段B
1C另一交点为E,连接A
1E,求:S
△A1DE:S
四边形AOBC的值.
查看答案和解析>>

 如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G. 作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G. ,
, )].
)]. ,
,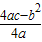 )].
)].
 ,
, )].
)].
 ,
, )].
)].
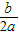 ,
, )].
)].
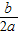 ,
, )].
)].
 ,
, )].
)].
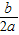 ,
,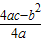 )].
)].
 ,
, )].
)].

 如图,过点C(0,-2)的抛物线y=ax2+bx+c的顶点M坐标为(2,-3),过点C作CB∥x轴交抛物线于点B,点P在线段BC上,CP=m.
如图,过点C(0,-2)的抛物线y=ax2+bx+c的顶点M坐标为(2,-3),过点C作CB∥x轴交抛物线于点B,点P在线段BC上,CP=m. ,
,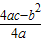 )].
)].
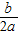 ,
,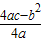 )].
)].
 ,
, )].
)].
 ,
, )].
)].
 已知二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,若点A的坐标是(1,0),点B在点A的右侧.
已知二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,若点A的坐标是(1,0),点B在点A的右侧. 如图:直线y=-
如图:直线y=- x+4m(常数m>0)交x轴于A点、交y轴于B点,四边形AOBC是以OA、OB为边的梯形,OA∥BC.将梯形AOBC逆时针旋转90°到A1OB1C1,连接B1C交y轴于D.(如图)
x+4m(常数m>0)交x轴于A点、交y轴于B点,四边形AOBC是以OA、OB为边的梯形,OA∥BC.将梯形AOBC逆时针旋转90°到A1OB1C1,连接B1C交y轴于D.(如图) x+4m(常数m>0)交x轴于A点、交y轴于B点,四边形AOBC是以OA、OB为边的梯形,OA∥BC.将梯形AOBC逆时针旋转90°到A1OB1C1,连接B1C交y轴于D.(如图)
x+4m(常数m>0)交x轴于A点、交y轴于B点,四边形AOBC是以OA、OB为边的梯形,OA∥BC.将梯形AOBC逆时针旋转90°到A1OB1C1,连接B1C交y轴于D.(如图)
 如图:直线y=-
如图:直线y=-