
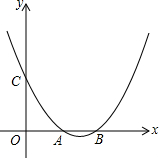
 已知二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,若点A的坐标是(1,0),点B在点A的右侧.
已知二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,若点A的坐标是(1,0),点B在点A的右侧.| b |
| 2a |
| 1-a |
| a |
| a+1 |
| a |
| b |
| 2a |
 (3)解方程:ax2-(a+1)x+1=0,
(3)解方程:ax2-(a+1)x+1=0,| 1 |
| a |
| 1-a |
| a |
| a+1 |
| a |
| a+1 |
| a |
| 1 |
| 2 |
| a+1 |
| a |
| 1 |
| 2 |
| 1-a |
| a |


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
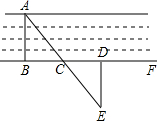 要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )| A、边角边 | B、角边角 |
| C、边边边 | D、边边角 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
| 5 |
| 9 |
| 7 |
| 12 |
| 1 |
| 36 |
| 18 |
| 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:
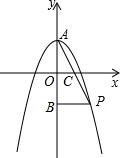 如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,若AC=PC,且S△AOC=1,记点A关于x轴的对称点为B.连结BP.
如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,若AC=PC,且S△AOC=1,记点A关于x轴的对称点为B.连结BP.查看答案和解析>>
科目:初中数学 来源: 题型:
| 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | |
| 第一行 | 2 | 4 | 6 | 8 | |
| 第二行 | 16 | 14 | 12 | 10 | |
| 第三行 | 18 | 20 | 22 | 24 | |
| 第四行 | … | … | 28 | 26 | |
| … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com