点C.D不与点O重合.求证AC⊥BD.AC=BD答案解析
科目:czsx
来源:
题型:

如图,在△ABC中,AB=AC,点D(不与点B重合)在BC上,点E是AB的中点,过点A作AF∥BC交DE延长线于点F,连接AD,BF.
(1)求证:△AEF≌△BED.
(2)若BD=CD,求证:四边形AFBD是矩形.
查看答案和解析>>
科目:czsx
来源:
题型:
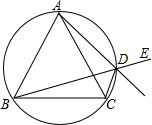
已知△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与点A重合),延长BD到E.
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30°,△ABC中BC边上的高为2+
.求△ABC的外接圆的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
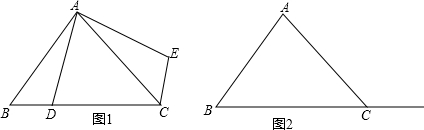
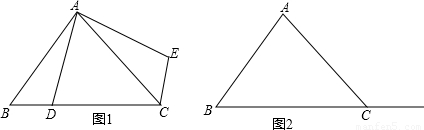
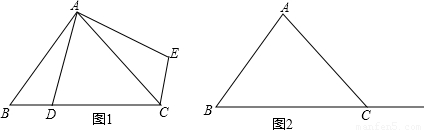
在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连接EC.
(1)如果AB=AC,∠BAC=90°
①当点D在线段BC上时(不与点B重合),如图1,请你判断线段CE,BD之间的位置关系和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2中画出图形,并判断①中的结论是否仍然成立,并证明你的判断.
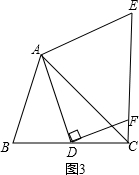
(2)如图3,若点D在线段BC上运动,DF⊥AD交线段CE于点F,且∠ACB=45°,
AC=3,试求线段CF长的最大值.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连接EC.
(1)如果AB=AC,∠BAC=90°
①当点D在线段BC上时(不与点B重合),如图1,请你判断线段CE,BD之间的位置关系和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2中画出图形,并判断①中的结论是否仍然成立,并证明你的判断.
(2)如图3,若点D在线段BC上运动,DF⊥AD交线段CE于点F,且∠ACB=45°,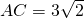 ,试求线段CF长的最大值.
,试求线段CF长的最大值.


查看答案和解析>>
科目:czsx
来源:2011-2012学年北京市丰台三中九年级(上)期末数学模拟试卷(解析版)
题型:解答题
在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连接EC.
(1)如果AB=AC,∠BAC=90°
①当点D在线段BC上时(不与点B重合),如图1,请你判断线段CE,BD之间的位置关系和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2中画出图形,并判断①中的结论是否仍然成立,并证明你的判断.
(2)如图3,若点D在线段BC上运动,DF⊥AD交线段CE于点F,且∠ACB=45°,

,试求线段CF长的最大值.


查看答案和解析>>
科目:czsx
来源:2011-2012学年广东省深圳市九年级(上)期中数学试卷(解析版)
题型:解答题
在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连接EC.
(1)如果AB=AC,∠BAC=90°
①当点D在线段BC上时(不与点B重合),如图1,请你判断线段CE,BD之间的位置关系和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2中画出图形,并判断①中的结论是否仍然成立,并证明你的判断.
(2)如图3,若点D在线段BC上运动,DF⊥AD交线段CE于点F,且∠ACB=45°,

,试求线段CF长的最大值.
查看答案和解析>>
科目:czsx
来源:2010-2011学年北京市东城区九年级(上)期末数学试卷(解析版)
题型:解答题
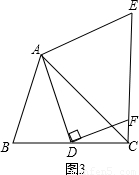
在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连接EC.
(1)如果AB=AC,∠BAC=90°
①当点D在线段BC上时(不与点B重合),如图1,请你判断线段CE,BD之间的位置关系和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2中画出图形,并判断①中的结论是否仍然成立,并证明你的判断.
(2)如图3,若点D在线段BC上运动,DF⊥AD交线段CE于点F,且∠ACB=45°,

,试求线段CF长的最大值.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连接EC.
(1)如果AB=AC,∠BAC=90°
①当点D在线段BC上时(不与点B重合),如图1,请你判断线段CE,BD之间的位置关系和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2中画出图形,并判断①中的结论是否仍然成立,并证明你的判断.
(2)如图3,若点D在线段BC上运动,DF⊥AD交线段CE于点F,且∠ACB=45°,
AC=3,试求线段CF长的最大值.


查看答案和解析>>
科目:czsx
来源:
题型:解答题
 菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
(1)比较∠F和∠ABD的大小,并说明理由;
(2)当△BFC有一个内角是直角时,求证:△BFC∽△EFA;
(3)当△BFC与△EFA相似(两三角形的公共角为对应角),且AC=12,DE=5时,求△BFC与△EFA的相似比.
查看答案和解析>>
科目:czsx
来源:
题型:
菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
(1)比较∠F和∠ABD的大小,并说明理由;
(2)当△BFC有一个内角是直角时,求证:△BFC∽△EFA;
(3)当△BFC与△EFA相似(两三角形的公共角为对应角),且AC=12,DE=5时,求△BFC与△EFA的相似比.

查看答案和解析>>
科目:czsx
来源:2013年湖北省宜昌市中考数学调研试卷(4月份)(解析版)
题型:解答题
菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
(1)比较∠F和∠ABD的大小,并说明理由;
(2)当△BFC有一个内角是直角时,求证:△BFC∽△EFA;
(3)当△BFC与△EFA相似(两三角形的公共角为对应角),且AC=12,DE=5时,求△BFC与△EFA的相似比.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
15.在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DE⊥AB,垂足为E,连接AD,将△DEB沿直线DE翻折得到△DEF,点B落在射线BA上的F处.
(1)求证:△DEB∽△ACB;
(2)当点F与点A重合时(如图①),求线段BD的长;
(3)设BD=x,AF=y,求y关于x的函数解析式,并判断是否存在这样的点D,使AF=FD?若存在,请求出x的值;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
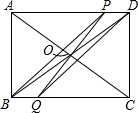
如图,矩形ABCD中,对角线AC、BD相交于O点,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=3cm,AD=4cm,P从点A出发.以1cm/秒的速度向点D匀速运动.设点P运动时间为t秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,矩形ABCD中,对角线AC、BD相交于点O,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于点Q.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=3cm,AD=4cm,P从点A出发.以1cm/秒的速度向点D匀速运动.设点P运动时间为 秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的
秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的 值;如果不能,说明理由.
值;如果不能,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.

查看答案和解析>>
科目:czsx
来源:2014-2015学年四川省丹棱县九年级第一次诊断性考试数学试卷(解析版)
题型:解答题
在菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.

(1)比较∠F和∠ABD的大小,并说明理由;
(2)当△BFC有一个内角是直角时,求证:△BFC∽△EFA;
(3)当△BFC与△EFA相似(两三角形的公共角为对应角),且AC=12,DE=5时,求△BFC与△EFA的相似比.
查看答案和解析>>
科目:czsx
来源:2015年初中毕业升学考试(湖北宜昌卷)数学(解析版)
题型:解答题
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
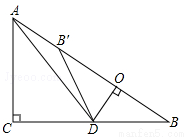
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
7.如图,在▱ABCD中,对角线AC与BD相交于点O,过点O作OE⊥CD,垂足为E,将线段OE绕点O逆时针旋转90°后得到线段OE′,已知OE=12,sin∠BAC=$\frac{12}{13}$.
(1)求AC的长;
(2)当F为射线ED上任意一点(点F不与点E重合)时,连接OF,将线段OF绕点O逆时针旋转90°得到线段OF′.试判断直线E′F′与直线CD的位置关系,并加以证明;
(3)在(2)的条件下,设EF=x,S
△AEF=y,求y与x之间的函数关系式,并写出自变量x的取值范围.
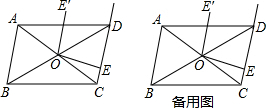
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.
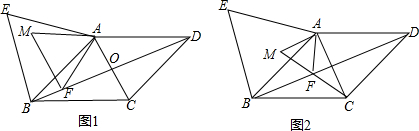
(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.

(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC= AM;
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
查看答案和解析>>

 如图,在△ABC中,AB=AC,点D(不与点B重合)在BC上,点E是AB的中点,过点A作AF∥BC交DE延长线于点F,连接AD,BF.
如图,在△ABC中,AB=AC,点D(不与点B重合)在BC上,点E是AB的中点,过点A作AF∥BC交DE延长线于点F,连接AD,BF. 已知△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与点A重合),延长BD到E.
已知△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与点A重合),延长BD到E.

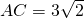 ,试求线段CF长的最大值.
,试求线段CF长的最大值.

 ,试求线段CF长的最大值.
,试求线段CF长的最大值.

 ,试求线段CF长的最大值.
,试求线段CF长的最大值.

 ,试求线段CF长的最大值.
,试求线段CF长的最大值.



 菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.


 如图,矩形ABCD中,对角线AC、BD相交于O点,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于Q点.
如图,矩形ABCD中,对角线AC、BD相交于O点,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于Q点. 秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的
秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的 值;如果不能,说明理由.
值;如果不能,说明理由.






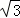 AM;
AM;