
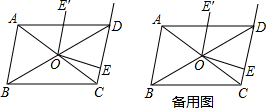
分析 (1)由四边形ABCD是平行四边形得到∠OCE=∠BAC,利用三角函数即可;
(2)由△EOF≌△E′OF′,得到∠F′E′O=∠OEF=90°,从而判断出垂直;
(3)分三种情况讨论(a)当点F在线段EG上时,可得y=$\frac{1}{2}$x(12-x)=-$\frac{1}{2}$x2+6x,x的取值范围为0<x<12.(b)当点F在EG的延长线上时,y=$\frac{1}{2}$x(x-12)=$\frac{1}{2}$x2-6x,x的取值范围为x>12.(c)当点F与点G重合时,△E′FF′不存在.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AC=2OC,
∴∠OCE=∠BAC,
∴sin∠OCE=sin∠BAC=$\frac{12}{13}$.
在Rt△OCE中,
∵OE=12,
∴OC=13.
∴AC=2OC=26;
(2)垂直;
证明:∠EOF=∠E′OF′.
又∵OE=OE′,OF=OF′,
∴△EOF≌△E′OF′,
∴∠F′E′O=∠OEF=90°,
∴E′F′所在的直线与OE平行,
∴直线E′F′与直线CD的位置关系是垂直.
(3)设直线E′F′
与直线CD的交点为G.易得四边形OEGE′是正方形,
∴EG=12.
(a)当点F在线段EG上时,
可得y=$\frac{1}{2}$x(12-x)=-$\frac{1}{2}$x2+6x,x的取值范围为0<x<12.
(b)当点F在EG的延长线上时,
y=$\frac{1}{2}$x(x-12)=$\frac{1}{2}$x2-6x,x
的取值范围为x>12.
(c)当点F与点G重合时,△E′FF′不存在.
综上所述:y与x的函数关系式为
y=-$\frac{1}{2}$x2+6x(0<x<12)和y=$\frac{1}{2}$x2-6x(x>12).
点评 此题是几何变换的综合题,主要考查旋转中的动点问题,旋转的性质的灵活运用是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com