
科目:czyw 来源:上海同步题 题型:阅读理解与欣赏
科目:czzz 来源: 题型:材料分析题
 数学运算离不开“+”号,在人生道路上,同样需要“+”号。请你运用所学知识完成下列加式。
数学运算离不开“+”号,在人生道路上,同样需要“+”号。请你运用所学知识完成下列加式。科目:czzz 来源:2015届广东省增城市八年级上学期期末考试政治试卷(解析版) 题型:单选题
某同学数学成绩很好,但在期中考试中没考出好成绩,遭到了挫折,便心烦意乱,吃不下饭,睡不好觉,结果得了重病住进医院,耽误了时间,不但数学成绩下降,也影响了其他功课的学习。这名同学对竞争的态度是
A积极的,能认真分析导致失败的原因,总结教训
B.消极的,能理智的对待竞争,面对失败不气馁
C.积极的,能勇敢地经受失败的考验
D.消极的,畏惧竞争,遇到失败就灰心丧气
科目:czzz 来源:同步题 题型:单选题
科目:gzsx 来源: 题型:
| 课 程[来 | 初等代数 | 平面几何 | 初等数论 | 微积分初步 | ||||||||
| 合格的概率 |
|
|
|
|
科目:gzsx 来源: 题型:
在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人去参加市级培训,在下列条件下,有多少种不同的选法?
(1)任意选5人;(2)甲、乙、丙三人必须参加;(3)甲、乙、丙三人不能参加;
(4)甲、乙、丙三人只能有1人参加;(5)甲、乙、丙三人至 少1人参加.
少1人参加.
科目:gzsx 来源: 题型:
a≥-
|
[140,150] | 合计 | |||
| 参加培训 | 5 | 8 | |||
| 未参加培训 | |||||
| 合计 | 4 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:gzsx 来源: 题型:
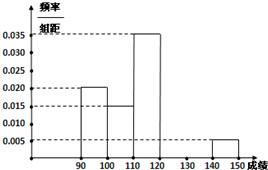
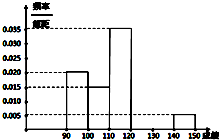 某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.| [120,140) | [140,150] | 合计 | |
| 参加培训 | 5 | 8 | |
| 未参加培训 | |||
| 合计 | 4 |
科目:czzz 来源:同步轻松练习(七年级思想品德上) 题型:013
宋扬这次数学考试考了全班第一,可他在总结中说:“从分数上看,我是第一,但从对题目的分析思路和解题技巧上看,刘静同学比我更胜一筹,我要向她学习。”可见宋扬同学。
A.能够总结缺点教训,是个十全十美的好学生
B.只看到自己的缺点,没有看到自己的长处
C.是个虚伪的同学,是谦虚过度的表现
D.能够从与他人的比较中正确认识自己
科目:gzsx 来源:2014届四川省高三“零诊”理科数学试卷(解析版) 题型:解答题
德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
|
课 程 |
初等代数 |
初等几何 |
初等数论 |
微积分初步 |
|
合格的概率 |
|
|
|
|
(1)求甲同学取得参加数学竞赛复赛的资格的概率;
(2)记 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求 的分布列及期望
的分布列及期望 .
.
科目:gzsx 来源:2012-2013学年安徽省高三第七次模拟考试文科数学试卷(解析版) 题型:解答题
某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分为150分),将成绩按如下方式分成六组,第一组 、第二组
、第二组 、第六组
、第六组 . 下图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 下图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.

(Ⅰ)求第四和第五组频率,并补全频率分布直方图;
(Ⅱ)若不低于120分的同学进入决赛,不低于140分的同学为种子选手,完成下面 列联表(即填写空格处的数据),并判断是否有99﹪的把握认为“进入决赛的同学成为种子选手与专家培训有关”.
列联表(即填写空格处的数据),并判断是否有99﹪的把握认为“进入决赛的同学成为种子选手与专家培训有关”.
|
|
|
|
合计 |
|
参加培训 |
5 |
|
8 |
|
未参加培训 |
|
|
|
|
合计 |
|
4 |
|
附:
|
|
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
科目:gzsx 来源: 题型:解答题
德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
| 课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
| 合格的概率 | 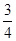 | 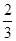 | 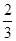 | 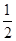 |
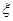 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求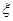 的分布列及期望
的分布列及期望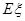 .
. 科目:gzsx 来源:不详 题型:解答题
| 课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
| 合格的概率 |  |  |  |  |
 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求 的分布列及期望
的分布列及期望 .
.科目:czyw 来源:同步题 题型:阅读理解与欣赏
科目:gzsx 来源: 题型:解答题

 | [140,150] | 合计 | |
| 参加培训 | 5 | 8 | |
| 未参加培训 | |||
| 合计 | 4 |
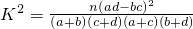
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:gzsx 来源:不详 题型:解答题

a≥-
|
[140,150] | 合计 | |||
| 参加培训 | 5 | 8 | |||
| 未参加培训 | |||||
| 合计 | 4 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:gzsx 来源: 题型:
某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组![]() 、第二组
、第二组![]() …第六组
…第六组![]() . 图(1)为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 图(1)为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.

(Ⅰ)请补充完整频率分布直方图,并估计这组数据的平均数M;
(Ⅱ)若不低于120分的同学进入决赛,不低于140分的同学为种子选手,完成下面![]() 列联表(即填写空格处的数据),并判断是否有99﹪的把握认为“进入决赛的同学成为种子选手与专家培训有关”.
列联表(即填写空格处的数据),并判断是否有99﹪的把握认为“进入决赛的同学成为种子选手与专家培训有关”.
|
| 合计 | |
参加培训 | 5 | 8 | |
未参加培训 | |||
合计 | 4 |
附:![]()
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:gzsx 来源:2010-2011学年吉林省吉林市高三(下)期中数学试卷(文科)(解析版) 题型:解答题

 | [140,150] | 合计 | |
| 参加培训 | 5 | 8 | |
| 未参加培训 | |||
| 合计 | 4 |

| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:gzsx 来源:2013年安徽师大附中高考数学七模试卷(文科)(解析版) 题型:解答题

 | [140,150] | 合计 | |
| 参加培训 | 5 | 8 | |
| 未参加培训 | |||
| 合计 | 4 |

| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |