
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2012年浙江省金华市义乌市中考数学模拟试卷(六)(解析版) 题型:解答题

科目:czsx 来源:2014-2015学年浙江省金华市九年级12月阶段检测数学试卷(解析版) 题型:解答题
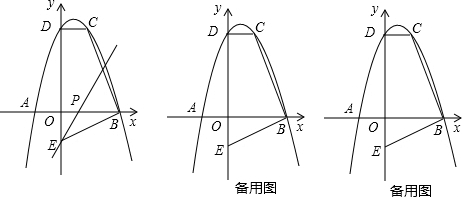
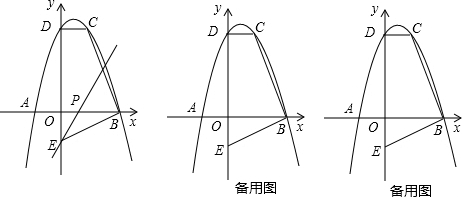
(本题12分)如图,平面直角坐标系中,O为坐标原点,抛物线 经过
经过 ,
, 两点,与y轴交于点D,与x轴交于另一点B.点E坐标为
两点,与y轴交于点D,与x轴交于另一点B.点E坐标为 ,点P是线段BO上的一个动点,从点B开始以1个单位每秒的速度沿BO向终点O运动;
,点P是线段BO上的一个动点,从点B开始以1个单位每秒的速度沿BO向终点O运动;

(1)求此抛物线的解析式;
(2)设运动时间为t秒,直线PE扫过四边形ABCD的面积为S,当直线PE与线段BC有交点时,求S关于t的函数关系式;
(3)能否将△OEB绕平面内某点旋转90°后使得△OEB的两个顶点落在抛物线上?若能,请直接写出旋转中心的坐标;若不能,请说明理由.
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
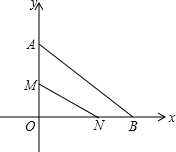 (2013•来宾)在△AOB中,∠AOB=90°,AO=6厘米,BO=8厘米,分别以OB和OA所在直线为x轴,y轴建立平面直角坐标系,如图所示,动点M从点A开始沿AO方向以2厘米/秒的速度向点O移动,同时动点N从点O开始沿OB方向以4厘米/秒的速度向点B移动(其中一点到达终点时,另一点随即停止移动).
(2013•来宾)在△AOB中,∠AOB=90°,AO=6厘米,BO=8厘米,分别以OB和OA所在直线为x轴,y轴建立平面直角坐标系,如图所示,动点M从点A开始沿AO方向以2厘米/秒的速度向点O移动,同时动点N从点O开始沿OB方向以4厘米/秒的速度向点B移动(其中一点到达终点时,另一点随即停止移动).科目:czsx 来源: 题型:
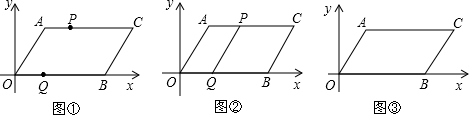
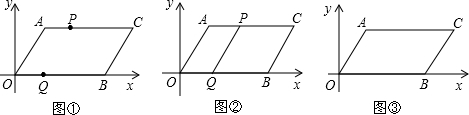
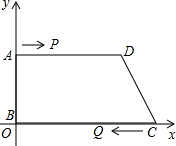 如图,直角梯形ABCD放在平面直角坐标系中,A(0,5),B(0,0),C(26,0),D(24,5)动点P,从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问:
如图,直角梯形ABCD放在平面直角坐标系中,A(0,5),B(0,0),C(26,0),D(24,5)动点P,从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问:科目:czsx 来源: 题型:
 如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么
如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么科目:czsx 来源: 题型:
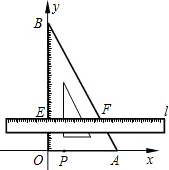 如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3| 3 |
| 3 |
| ||
| 3 |
科目:czsx 来源: 题型:
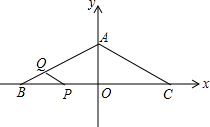 如图,在等腰三角形ABC中,AB=AC=10cm,∠ABC=30°,以BC所在直线为x轴,以BC边上的高所在的直线为y轴建立平面直角坐标系.
如图,在等腰三角形ABC中,AB=AC=10cm,∠ABC=30°,以BC所在直线为x轴,以BC边上的高所在的直线为y轴建立平面直角坐标系.科目:czsx 来源:2010年浙江省金华市初中毕业生学业考试数学试卷 题型:059
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3![]() ).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民.数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,
).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民.数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,![]() ,2(长度单位/秒).一直尺的上边缘l从x轴的位置开始以
,2(长度单位/秒).一直尺的上边缘l从x轴的位置开始以![]() (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点.设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点.设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
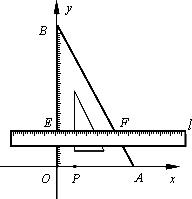
请解答下列问题:
(1)过A,B两点的直线解析式是________;
(2)当t﹦4时,点P的坐标为________;当t﹦________,点P与点E重合;
(3)①作点P关于直线EF的对称点![]() 在运动过程中,若形成的四边形PE
在运动过程中,若形成的四边形PE![]() F为菱形,则t的值是多少?
F为菱形,则t的值是多少?
②当t﹦2时,是否存在着点Q,使得△FEQ∽△BEP?若存在,求出点Q的坐标;若不存在,请说明理由.
科目:czsx 来源: 题型:解答题
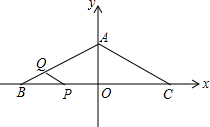 如图,在等腰三角形ABC中,AB=AC=10cm,∠ABC=30°,以BC所在直线为x轴,以BC边上的高所在的直线为y轴建立平面直角坐标系.
如图,在等腰三角形ABC中,AB=AC=10cm,∠ABC=30°,以BC所在直线为x轴,以BC边上的高所在的直线为y轴建立平面直角坐标系.科目:czsx 来源: 题型:解答题
 x+6的图象交于点A.动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
x+6的图象交于点A.动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S. 条件是______.
条件是______.科目:czsx 来源:同步题 题型:解答题
如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么
(1)设△POQ的面积为y,求y关于t的函数解析式;
(2)当△POQ的面积最大时,将△POQ沿直线PQ翻折后得到△PCQ,试判断点C是否落在直线AB上,并说明理由;
(3)当t为何值时,△POQ与△AOB相似.

科目:czsx 来源: 题型:
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3![]() ).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为1,
).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为1,![]() ,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
请解答下列问题:
1.过A,B两点的直线解析式是 ▲
2.当t﹦4时,点P的坐标为 ▲ ;当t ﹦ ▲ ,点P与点E重合;
3.① 作点P关于直线EF的对称点P′. 在运动过程中,若形成的四边形PEP′F为菱形,则t的值是多少?
② 当t﹦2时,是否存在着点Q,使得△FEQ ∽△BEP ?若存在, 求出点Q的坐标;若不存在,请说明理由.

科目:czsx 来源: 题型:
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,
,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
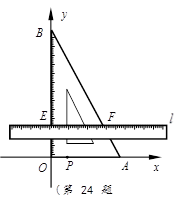
请解答下列问题:
(1)过A,B两点的直线解析式是 ▲ ;
(2)当t﹦4时,点P的坐标为 ▲ ;当t ﹦ ▲ ,点P与点E重合;
(3)
① 作点P关于直线EF的对称点P′. 在运动过程中,若形成的四边形PEP′F为菱形,则t的值是多少?
② 当t﹦2时,是否存在着点Q,使得△FEQ ∽△BEP ?若存在, 求出点Q的坐标;
若不存在,请说明理由.
科目:czsx 来源: 题型:
 ).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,
).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1, ,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
科目:czsx 来源:2010年高级中等学校招生全国统一考试数学卷(山东莱芜) 题型:解答题
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3 ).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,
).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1, ,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
请解答下列问题:
(1)过A,B两点的直线解析式是 ▲ ;
(2)当t﹦4时,点P的坐标为 ▲ ;当t ﹦ ▲ ,点P与点E重合;
(3)
① 作点P关于直线EF的对称点P′. 在运动过程中,若形成的四边形PEP′F为菱形,则t的值是多少?
② 当t﹦2时,是否存在着点Q,使得△FEQ ∽△BEP ?若存在, 求出点Q的坐标;
若不存在,请说明理由.