练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >如图.三角形ABC是等腰三角形.D.E分别是腰AB

    如图.三角形ABC是等腰三角形.D.E分别是腰AB答案解析

    科目：czsx 来源：三点一测丛书九年级数学上 题型：047

    如图，已知△ABC是等腰三角形，D、E分别是腰AC、AB的中点，求证BD＝CE．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图所示，△ABC是等腰三角形，D，E分别是腰AB及AC延长线上的一点，且BD=CE，连接DE交底BC于G．求证：GD=GE．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图所示，△ABC是等腰三角形，D，E分别是腰AB及腰AC延长线上的一点，且BD=CE，连接DE交底BC于G．求证：GD=GE．

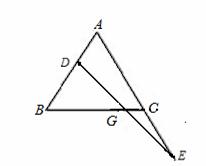
    查看答案和解析>>

    科目：czsx 来源： 题型：

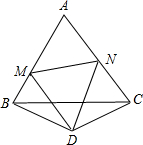
    精英家教网如图，已知△ABC是等边三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°角它的两边分别交AB于M，交AC于N，连接MN，求证：MN=BM+CN．

    查看答案和解析>>

    科目：czsx 来源：2012年北师大版初中数学九年级下2.7最大面积是多少练习卷（解析版） 题型：解答题

    如图,已知△ABC是一等腰三角形铁板余料,其中AB=AC=20cm,BC=24cm.若在△ABC上截出一矩形零件DEFG,使EF在BC上,点D、G分别在边AB、AC上.问矩形DEFG的最大面积是多少?

     

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

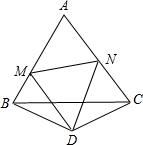    如图，已知△ABC是等边三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°角它的两边分别交AB于M，交AC于N，连接MN，求证：MN=BM+CN．

    查看答案和解析>>

    科目：czsx 来源：2009-2010学年山西省太原市九年级（上）期中数学试卷（解析版） 题型：解答题

    如图，已知D是等腰三角形ABC底边BC上的一点，它到两腰AB、AC的距离分别为DE、DF，请指出当D在什么位置时，DE=DF，并加以证明．

    查看答案和解析>>

    科目：czsx 来源：不详 题型：解答题

    如图，已知△ABC是等边三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°角它的两边分别交AB于M，交AC于N，连接MN，求证：MN=BM+CN．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图所示，△ABC是等腰直角三角形，∠BAC=90°，AB=AC．
    （1）若D为BC的中点，过D作DM⊥DN分别交AB、AC于M、N，求证：DM=DN；
    （2）若DM⊥DN分别和BA、AC延长线交于M、N，问DM和DN有何数量关系，并证明．

    查看答案和解析>>

    科目：czsx 来源： 题型：

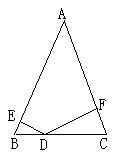
    21、如图，已知D是等腰三角形ABC底边BC上的一点，它到两腰AB、AC的距离分别为DE、DF，请指出当D在什么位置时，DE=DF，并加以证明．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图，已知△ABC是等腰直角三角形，AB=AC，AD是斜边的中线，E、F分别是AB、AC边上的点，精英家教网且DE⊥DF，若BE=8，CF=6．
    （1）求证：△AED≌△CFD；
    （2）求△DEF的面积．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    精英家教网如图，△ABC是等腰三角形，D，E分别是腰AB及AC延长线上的一点，且BD=CE，连接DE交底BC于G．求证GD=GE．

    查看答案和解析>>

    科目：czsx 来源：1+1轻巧夺冠·优化训练·九年级数学下（北京课改版）·银版 题型：059

    如图，已知△ABC是等腰直角三角形，∠C＝90°

    (1)操作并观察，如图，将三角板的45°角的顶点与点C重合，使这个角落在∠ACB的内部，两边分别与斜边AB交于E、F两点，然后将这个角绕着点C在∠ACB的内部旋转，观察在点E、F的位置发生变化时，AE、EF、FB中最长线段是否始终是EF？试写出观察结果．

    (2)探索：AE、EF、FB这三条线段能否组成以EF为斜边的直角三角形(即能否有EF2＝AE2＋BF2)？如果能，试加以证明．

    查看答案和解析>>

    科目：czsx 来源：学习周报　数学　沪科九年级版　2009－2010学年　第7期　总第163期 沪科版 题型：044

    如图，△ABC是一块等腰三角形的废铁料(AB＝AC)．已知∠BAC是锐角，量得底边BC的长为60 cm，BC边上的高为40 cm，用它截一块一边长为30 cm的矩形(要求：使矩形的一边与△ABC的一边重合，而矩形的另两个顶点分别在△ABC的另两条边上)．

    (1)问一共有几种不同的截法，请在图中画出所有截法的示意图，并在图中标明长为30 cm的那条边；

    (2)试求出以上你所画的各种截法中，所截得的矩形的另一边长．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

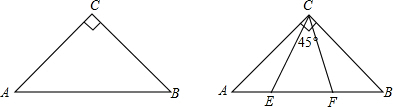
    如图，已知△ABC是等腰直角三角形，∠C=90度．
    （1）操作并观察，如图，将三角板的45°角的顶点与点C重合，使这个角落在∠ACB的内部，两边分别与斜边AB交于E、F两点，然后将这个角绕着点C在∠ACB的内部旋转，观察在点E、F的位置发生变化时，AE、EF、FB中最长线段是否始终是EF？写出观察结果．
    （2）探索：AE、EF、FB这三条线段能否组成以EF为斜边的直角三角形？如果能，试加以证明．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

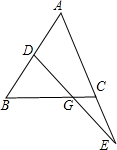    如图，△ABC是等腰三角形，D，E分别是腰AB及AC延长线上的一点，且BD=CE，连接DE交底BC于G．求证GD=GE．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    如图，已知△ABC是等腰直角三角形，AB=AC，AD是斜边的中线，E、F分别是AB、AC边上的点，且DE⊥DF，若BE=8，CF=6．
    （1）求证：△AED≌△CFD；
    （2）求△DEF的面积．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图13.1，△ABC是等腰直角三角形，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD＝CF，BD⊥CF成立.

    （1）当正方形ADEF绕点A逆时针旋转θ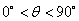（）时，如图13.2，BD＝CF成

    立吗？若成立，请证明；若不成立，请说明理由.

    （2）当正方形ADEF绕点A逆时针旋转45°时，如图13.3，延长BD交CF于点G.

    ① 求证：BD⊥CF；

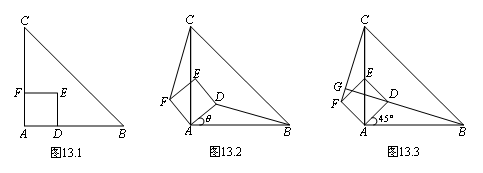    ② 当AB＝4，AD＝时，求线段BG的长.

    查看答案和解析>>

    科目：czsx 来源：2012年广东省汕头市潮阳区中考数学模拟试卷（二）（解析版） 题型：解答题

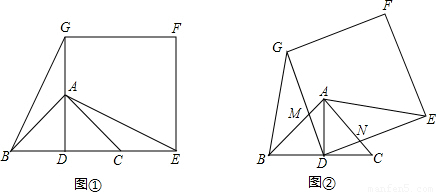
    如图①，已知△ABC是等腰直角三角形，∠BAC=90°，BC=2，AD是BC边上的高．作正方形DEFG，使点A、C分别在DG和DE上，且DE=BC，且连接AE、BG．
    （1）试猜想线段BG和AE的数量关系，请直接写出你得到的结论；
    （2）将正方形DEFG绕点D逆时针方向旋转一定角度后（旋转角度大于0°，或小于90°），DG、DE分别交AB、AC于点M和N（如图②），则（1）中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由．
    （3）在（2）的情况下，当AE∥BC时，求AM的值．

    查看答案和解析>>

    科目：czsx 来源：2011年广东省湛江市中考数学模拟试卷（五）（解析版） 题型：解答题

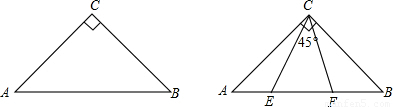
    如图，已知△ABC是等腰直角三角形，∠C=90度．
    （1）操作并观察，如图，将三角板的45°角的顶点与点C重合，使这个角落在∠ACB的内部，两边分别与斜边AB交于E、F两点，然后将这个角绕着点C在∠ACB的内部旋转，观察在点E、F的位置发生变化时，AE、EF、FB中最长线段是否始终是EF？写出观察结果．
    （2）探索：AE、EF、FB这三条线段能否组成以EF为斜边的直角三角形？如果能，试加以证明．

    查看答案和解析>>