科目：czsx 来源： 题型：
与点E，连接BE、CE，BE交AC于点F．科目：czsx 来源： 题型：044
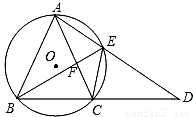
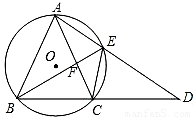
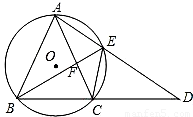
如图，⊙O是等腰三角形ABC的外接圆，AB=AC，延长BC至点D，使CD＝AC，连接AD交⊙O与点E，连接BE、CE与AC交于点F。
(1
）求证：△ABE≌△CDE；(2
）若AE=6，DE=9，求EF的长。
科目：czsx 来源：江苏省连云港市2006年中等学校招生统一考试数学试题 题型：044
如图，⊙O是等腰三角形ABC的外接圆，AB＝AC，延长BC至点D，使CD＝AC，连接AD交⊙O与点E，连接BE、CE与AC交于点F．
(1)求证：△ABE≌△CDE；
(2)若AE＝6，DE＝9，求EF的长．
科目：czsx 来源： 题型：解答题
与点E，连接BE、CE，BE交AC于点F．科目：czsx 来源：连云港 题型：解答题
科目：czsx 来源：第3章《圆》中考题集（23）：3.3 圆周角和圆心角的关系（解析版） 题型：解答题
科目：czsx 来源：第3章《圆》中考题集（22）：3.1 圆（解析版） 题型：解答题
科目：czsx 来源：第28章《圆》中考题集（22）：28.1 圆的认识（解析版） 题型：解答题
科目：czsx 来源：第26章《圆》中考题集（37）：26.4 圆周角（解析版） 题型：解答题
科目：czsx 来源：2012-2013学年湖北省黄冈市某校九年级（上）期中数学试卷（解析版） 题型：解答题
科目：czsx 来源：第3章《圆》中考题集（22）：3.3 圆周角（解析版） 题型：解答题
科目：czsx 来源：第22章《圆（上）》中考题集（26）：22.4 圆周角（解析版） 题型：解答题
科目：czsx 来源：第29章《相似形》中考题集（18）：29.5 相似三角形的性质（解析版） 题型：解答题
科目：czsx 来源：第5章《中心对称图形（二）》中考题集（20）：5.3 圆周角（解析版） 题型：解答题
科目：czsx 来源：第4章《相似三角形》中考题集（18）：4.3 两个三角形相似的判定（解析版） 题型：解答题
科目：czsx 来源：2006年江苏省连云港市中考数学试卷（课标卷）（解析版） 题型：解答题
科目：czsx 来源： 题型：
| 2 |
科目：czsx 来源：2014-2015学年江苏省泰州市姜堰区八年级上学期期中考试数学试卷（解析版） 题型：解答题
（本题12分）如图，△ABC和△CDE均为等腰三角形，AC=BC，CD=CE，AC>CD，∠ACB=∠DCE且点A、D、E在同一直线上，连接BE．
（1）若∠ACB=60°, 则∠AEB的度数为 ；
线段AD、BE之间的数量关系是 ．
（2）若∠ACB=∠DCE=90°, CM为△DCE中DE边上的高．
①求∠AEB的度数．
②若
，
，试求CM的长．（请写全必要的证明和计算过程）
科目：czsx 来源： 题型：
| 3 |
| 3 |
科目：czsx 来源： 题型：
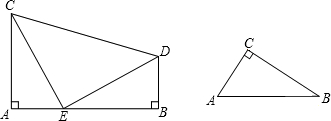
如图，已知：AC⊥AB，BD⊥AB，且AC=BE，AE=BD，求证：△CDE是等腰直角三角形；
证明：∵AC⊥AB，BD⊥AB ∴∠CAE=∠DBE=90°
∵AC= BE，AE=BD ∴△ACE≌△BED
∴CE=DE且∠ACE=∠BED
∵∠ACE+∠AEC=90° ∴∠AEC+∠BED=90°
∴∠CED=90° ∴△CED为等腰直角三角形
利用上题的解题思路解答下列问题：
在Rt△ABC中，∠C=90°，D，E分别为CB，CA延长线上的点，BE与AD的交点为P.
1.若BD=AC，AE=CD，在下图中画出符合题意的图形，求出∠APE的度数；
2.若AC=BD，CD=AE，则∠APE=__________°