
科目:gzsx 来源:2015-2016学年湖南师大附中高二上第一次段测文科数学卷(解析版) 题型:选择题
若存在正整数T,对于任意正整数n都有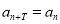 成立,则称数列
成立,则称数列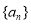 为周期数列,周期为T,已知数列
为周期数列,周期为T,已知数列 满足:
满足: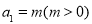 ,
, ,关于下列命题:
,关于下列命题:
①当 时,
时,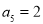 ;
;
②若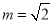 ,则数列
,则数列 是周期为3的数列;
是周期为3的数列;
③若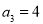 ,则m可以取3个不同的值;
,则m可以取3个不同的值;
④ 且
且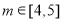 ,使得数列
,使得数列 的周期为6;
的周期为6;
其中真命题的个数是( )
A.1 B.2 C.3 D.4
科目:gzsx 来源:湖北省示范性高中孝昌二中2008届高三九月月考数学试卷(理科) 题型:044
已知数列{an}有a1=a,a2=p(常数p>0),对任意的正整数n,Sn=a1+a2+…+an,并有Sn满足![]() .
.
(1)求a的值;
(2)试确定数列{an}是否是等差数列,若是,求出其通项公式,若不是,说明理由;
(3)对于数列{bn},假如存在一个常数b使得对任意的正整数n都有bn<b,且![]() ,则称b为数列{bn}的“上渐近值”,令
,则称b为数列{bn}的“上渐近值”,令![]() ,求数列{p1+p2+…+pn-2n}的“上渐近值”.
,求数列{p1+p2+…+pn-2n}的“上渐近值”.
科目:gzsx 来源:2008-2009学年度高三数学模拟试题分类汇编:数列 题型:044
已知数列{an}有a1a=a,a2=p(常数p>0),对任意的正整数n,Sn=a1+a2+…+an,并有Sn满足![]() .
.
(1)求a的值;
(2)试确定数列{an}是否是等差数列,若是,求出其通项公式,若不是,说明理由;
(3)对于数列{bn},假如存在一个常数b使得对任意的正整数n都有bn<b,且![]() ,则称b为数列{bn}的“上渐近值”,令
,则称b为数列{bn}的“上渐近值”,令![]() ,求数列{p1+p2+…+pn-2n}的“上渐近值”.
,求数列{p1+p2+…+pn-2n}的“上渐近值”.
科目:gzsx 来源:辽宁省沈阳二中2008届高三第四次模拟考试(数学) 题型:044
已知数列{an}有a1=a,a2=p(常数 p>0),对任意的正整数n,Sn=a1+a2+…+an,并有Sn满足![]() .
.
(1)求a的值;
(2)试确定数列{an}是否是等差数列,若是,求出其通项公式,若不是,说明理由;
(3)(理科生答文科生不答)对于数列{bn},假如存在一个常数![]() 使得对任意的正整数n都有bn<b,且
使得对任意的正整数n都有bn<b,且![]() ,则称b为数列{bn}的“上渐近值”,令
,则称b为数列{bn}的“上渐近值”,令![]() ,求数列{p1+p2+…+pn-2n}的“上渐近值”.
,求数列{p1+p2+…+pn-2n}的“上渐近值”.
科目:gzsx 来源:浙江省杭州市学军中学2007-2008学年度第一学期期中考试高三数学试题(文) 题型:044
已知数列{an}满足:a1=a(a≠0,且a≠1),其前n项的和Sn=![]()
(Ⅰ)求证:{an}为等比数列
(Ⅱ)记bn=anlg|an|(n为正整数),Tn为数列{bn}的前n项和
(1)a=2,求Tn
(2)当a=-![]() 时,是否存在正整数m,使得对于任意的正整数n都有bn≥bm?如果存在,求出m的值,否则,说明理由.
时,是否存在正整数m,使得对于任意的正整数n都有bn≥bm?如果存在,求出m的值,否则,说明理由.
科目:gzsx 来源:2014年高考数学考前复习冲刺穿插滚动练习(三)(解析版) 题型:选择题
已知数列{an}满足a1= ,且对任意的正整数m,n,都有am+n=am·an,若数列{an}的前n项和为Sn,则Sn等于( )
,且对任意的正整数m,n,都有am+n=am·an,若数列{an}的前n项和为Sn,则Sn等于( )
A.2-( )n-1 B.2-(
)n-1 B.2-( )n
)n
C.2- D.2-
D.2-
科目:gzsx 来源: 题型:解答题
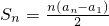 .
.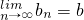 ,则称b为数列{bn}的“上渐进值”,求数列
,则称b为数列{bn}的“上渐进值”,求数列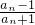 的“上渐进值”.
的“上渐进值”.科目:gzsx 来源: 题型:单选题
科目:gzsx 来源:上海模拟 题型:解答题
| n(an-a1) |
| 2 |
| lim |
| n→∞ |
| an-1 |
| an+1 |
科目:gzsx 来源:不详 题型:单选题
| 1 |
| 3 |
| lim |
| n→∞ |
A.
| B.
| C.
| D.2 |
科目:gzsx 来源:2012-2013学年山西省太原五中高三(上)12月月考数学试卷(理科)(解析版) 题型:选择题
 的值是( )
的值是( )科目:gzsx 来源:2012年陕西省西安市八校高三5月联考数学试卷(文科)(解析版) 题型:选择题
科目:gzsx 来源:2004-2005学年上海市十校高三联考数学试卷(文科)(解析版) 题型:解答题
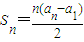 .
. ,则称b为数列{bn}的“上渐进值”,求数列
,则称b为数列{bn}的“上渐进值”,求数列 的“上渐进值”.
的“上渐进值”.科目:gzsx 来源:不详 题型:单选题
 ,且对任意的正整数m,n,都有am+n=am·an,若数列{an}的前n项和为Sn,则Sn等于( )
,且对任意的正整数m,n,都有am+n=am·an,若数列{an}的前n项和为Sn,则Sn等于( )A.2-( )n-1 )n-1 | B.2-( )n )n |
C.2- | D.2- |
科目:gzsx 来源: 题型:
| 1 |
| 4 |
科目:gzsx 来源: 题型:
| 2 |
| 3 |
A、2-(
| ||
B、2-(
| ||
C、2-
| ||
D、2-
|
科目:gzsx 来源: 题型:
| A、22014-1 |
| B、22014+1 |
| C、22015-1 |
| D、22015+1 |