
科目:czsx 来源: 题型:阅读理解
| A.好举里巷谐媟以为抚掌之资抚掌:拍手,表示高兴。 |
| B.经营粉本,高下浓淡经营:经度营造 |
| C.不事雕饰,雅合自然雅:文雅 |
| D.尺寸勿爽爽:差错 |
| A.尽其心力以求仿佛赵王岂以一璧之故欺秦邪 |
| B.则李工部之横云之二虫,又何知 |
| C.辄数见焉吴之民方痛心焉 |
| D.与人交,好谈人之善始可与言《诗》已矣 |
| A.本文所记述的张南垣尤擅长垒石造山,具有山水画的意境,构思巧妙,师法自然。 |
| B.本文例举了张南垣所建造园林的代表作及其建造过程,说明他的建造风格,并指出他的技艺符合园林建造的规律。 |
| C.本文还描写了张南垣的外貌性格,因为生得黑而矮胖,又喜欢拿街头巷尾荒唐不经的传说作为谈笑的资料,所以他自己也常常被人调笑耍弄,但他从不与人计较。 |
| D.全文语言流畅工丽,结构严谨,写人状物,如在目前。 |
科目:czsx 来源:2016届江苏省九年级上学期期中考试数学试卷(解析版) 题型:解答题
在一个不透明的箱子里,装有红、白、黑各一个球,它们除了颜色之外没有其他区别.
(1)随机地从箱子里取出1个球,则取出红球的概率是多少?
(2)随机地从箱子里取出1个球,放回搅匀再取第二个球,请你用画树状图或列表的方法表示所有等可能的结果,并求两次取出相同颜色球的概率.
【答案】(1) ;(2)
;(2)
【解析】
试题分析:(1)由在一个不透明的箱子里,装有红、白、黑各一个球,它们除了颜色之外没有其他区别,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次取出相同颜色球的情况,再利用概率公式即可求得答案.
试题解析: 【解析】
(1)∵在一个不透明的箱子里,装有红、白、黑各一个球,它们除了颜色之外没有其他区别,
∴随机地从箱子里取出1个球,则取出红球的概率是: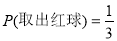 ;
;
(2)画树状图得:
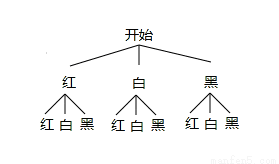
∵共有9种等可能的结果,两次取出相同颜色球的有3种情况,
∴两次取出相同颜色球的概率为: .
.
考点:概率
【题型】解答题
【适用】一般
【标题】2016届江苏省滨海县一中九年级上学期期中考试数学试卷(带解析)
【关键字标签】
【结束】
已知关于x的一元二次方程 .
.
(1)若 是此方程的一个根,求m的值;
是此方程的一个根,求m的值;
(2)试说明无论m取什么实数时,此方程总有实数根.
科目:czsx 来源: 题型:阅读理解
| A.十岁通五经通:通晓 | B.自蜀至长安,道未振振:振作 |
| C.白益傲放益:更加 | D.白时卧庐山,辟为僚佐辟:征召,被…聘用 |
| A.因以命之衡因上疏陈事 | B.以所业投贺知章何面目以归汉 |
| C.遂荐于玄宗而君幸于赵王 | D.白长笑而去天苍苍而高也 |
| A.②③④ | B.③④⑤ | C.①③④ | D.②③⑤ |
| A.李母梦见太白金星而生下李白,所以李白的名字中有“白”字。李白天赋过人,才华横溢。 |
| B.贺知章很欣赏李白的诗才,感叹他是遭贬的仙人。李白后经贺知章的推荐,担任翰林供奉。 |
| C.在朝廷上下,李白都表现出放荡不羁的个性,这说明李白是个决不“摧眉折腰事权贵”的人。 |
| D.郭子仪曾有恩于李白。后来,李白受牵连下狱,郭子仪又请求用自己的官爵来赎免李白的死罪。 |
科目:czsx 来源:2015年初中毕业升学考试(山东青岛卷)数学(解析版) 题型:解答题
(本小题满分10分)
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成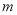 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当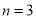 时,
时,
用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当 时,
时,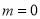
用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当 时,
时,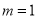
用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当 时,
时,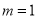
综上所述,可得表①
| 3 | 4 | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二:
用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用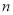 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设 分别等于
分别等于 、
、 、
、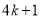 、
、 ,其中
,其中 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
科目:czsx 来源: 题型:
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成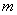 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究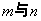 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当 时,
时,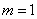
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当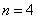 时,
时,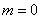
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当 时,
时,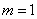
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当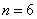 时,
时,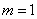
综上所述,可得表①
|
| 3 | 4 | 5 | 6 |
|
| 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2) 分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
|
| 7 | 8 | 9 | 10 |
|
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设 分别等于
分别等于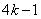 、
、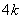 、
、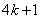 、
、 ,其中
,其中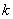 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
科目:czsx 来源:2015-2016学年山东省东营市恳利县八年级上学期期中考试数学试卷(解析版) 题型:解答题
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成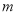 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究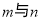 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当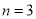 时,
时,
用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当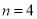 时,
时,
用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当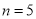 时,
时,
用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三 角形
角形
所以,当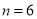 时,
时,
综上所述,可得表①
| 3 | 4 | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二:
用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(只需把结果填在表②中)
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设 分别等于
分别等于 、
、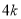 、
、 、
、 ,其中
,其中 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余 ),能搭成多少种不同的等腰三角形?(要求写出解答过程)
),能搭成多少种不同的等腰三角形?(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
科目:czsx 来源: 题型:
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形.所以,当n=3时,m=1
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形,所以,当n=4时,m=0
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形,所以,当n=5时,m=1
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=6时,m=1
综上所述,可得表①
| n | 3 | 4 | 5 | 6 |
| m | 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三
角形?(只需把结果填在表②中)
| n | 7 | 8 | 9 | 10 |
| m |
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
解决问题:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设n分别等于4k﹣1、4k、4k+1、4k+2,其中k是整数,把结果填在表 ③中)
| n | 4k﹣1 | 4k | 4k+1 | 4k+2 |
| m |
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________根木棒.(只填结果)
科目:czsx 来源:2015-2016学年山东省威海市七年级上期中数学试卷(解析版) 题型:解答题
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成 种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当 时,
时,
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当 时,
时,
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当 时,
时,
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当 时,
时,
综上所述,可得表①
| 3 | 4] | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三
角形?(只需把结果填在表②中)
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设 分别等于
分别等于 、
、 、
、 、
、 ,其中
,其中 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
科目:czsx 来源:2016-2017学年山东威海环翠区七年级五四制上期中考试数学卷(解析版) 题型:解答题
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当 时,
时,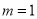
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当 时,
时,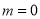
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当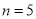 时,
时,
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当 时,
时,
综上所述,可得表①
| 3 | 4] | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三
角形?(只需把结果填在表②中)
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设 分别等于
分别等于 、
、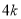 、
、 、
、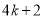 ,其中
,其中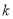 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
科目:czsx 来源: 题型:
近年来,大学生就业日益困难.为了扶持大学生自主创业,某市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其他费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
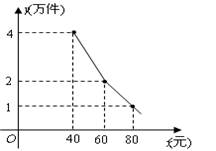
(1)分别求出40<x≤60;60<x<80时,月销售量y(万件)与销售
单价x(元)之间的函数关系;
(2)当销售单价定为50元时,为保证公司月利润达到5万元
(利润=销售额—生产成本—员工工资—其它费用),该公司
可安排员工多少人?
(3)若该公司有80名员工,则该公司最早可在几月后还清贷款?
【解析】(1)利用图象上点的坐标利用待定系数法代入y=kx+b,求出一次函数解析式即可;
(1) 根据利润=销售额—生产成本—员工工资—其它费用列方程求出解
(3)分两种情况进行讨论:当![]() 时,当
时,当![]() 时得出结论
时得出结论
科目:czsx 来源:2011-2012学年江苏省泰州市靖江外国语学校中考二模数学卷(解析版) 题型:解答题
近年来,大学生就业日益困难.为了扶持大学生自主创业,某市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其他费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
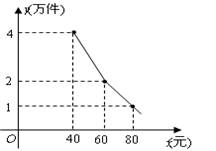
(1)分别求出40<x≤60;60<x<80时,月销售量y(万件)与销售
单价x(元)之间的函数关系;
(2)当销售单价定为50元时,为保证公司月利润达到5万元
可安排员工多少人?
(3)若该公司有80名员工,则该公司最早可在几月后还清贷款?
【解析】(1)利用图象上点的坐标利用待定系数法代入y=kx+b,求出一次函数解析式即可;
(1) 根据利润=销售额—生产成本—员工工资—其它费用列方程求出解
(3)分两种情况进行讨论:当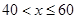 时,当
时,当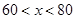 时得出结论
时得出结论
科目:czsx 来源: 题型:阅读理解
| A.欣少靖默,无竞于人竞:争斗 |
| B.称病自免,屏居里巷屏:隐退 |
| C.弟徽被遇于高祖遇:对待 |
| D.自非寻省近亲,不妄行诣诣:去、到 |
| A.献之书裙数幅而去后人哀之而不鉴之 |
| B.不以高卑见色以事秦之心礼天下之奇才 |
| C.殿中礼乐所出不者,若属皆且为所虏 |
| D.转在义兴,非其好也求木之长者,必固其根本 |
| A.羊欣在十二岁时就得到王献之的赏识,王献之在羊欣睡觉的时候,在羊欣的新绢裙上写了几幅字,羊欣的书法也因此得到进一步提高。 |
| B.会稽王世子元显经常让羊欣给他写字,羊欣坚决推辞,因而被贬为军府舍人,但羊欣却能泰然对之。 |
| C.羊欣多次被征召为官,但他却无意于仕途,或辞不就命,或称病自免,即便在任,也常以山水为娱。 |
| D.羊欣平常喜欢黄老之学,经常抄写黄老典籍,即使生病也不吃药,但他却精通医术,还撰写了十卷《药方》。 |