练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >X的平方+6X+4=0用公式法解

    X的平方+6X+4=0用公式法解答案解析

    科目：czsx 来源： 题型：

    解方程
    （1）2（x-3）2=8（直接开平方法）        （2）4x2-6x-3=0（运用公式法）
    （3）（2x-3）2=5（2x-3）（运用分解因式法）  （4）（x+8）（x+1）=-12（运用适当的方法）

    查看答案和解析>>

    科目：czsx 来源：《第22章 一元二次方程》2010年贵阳市开阳县宅吉中学单元测试卷（一）（解析版） 题型：解答题

    解方程
    （1）2（x-3）2=8（直接开平方法）        （2）4x2-6x-3=0（运用公式法）
    （3）（2x-3）2=5（2x-3）（运用分解因式法）  （4）（x+8）（x+1）=-12（运用适当的方法）

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    解方程
    （1）2（x-3）2=8（直接开平方法）　　　 （2）4x2-6x-3=0（运用公式法）
    （3）（2x-3）2=5（2x-3）（运用分解因式法） （4）（x+8）（x+1）=-12（运用适当的方法）

    查看答案和解析>>

    科目：czsx 来源： 题型：阅读理解

    阅读以下文字并解决问题：

         对于形如x2+2ax+a2这样的二次三项式，我们可以直接用公式法把它分解成（x+a）2 的形式，但对于二次三项式x2+6x-27,就不能直接用公式法分解了。此时，我们可以在x2+6x-27中间先加上一项9，使它与x2+6x的和构成一个完全平方式，然后再减去9，则整个多项式的值不变。 即：x2+6x-27=（x2+6x+9）-9-27=（x+3）2-62=（x+3+6）(x+3-6)=(x+9)(x-3),

    像这样，把一个二次三项式变成含有完全平方式的形式的方法，叫做配方法。

    （1）利用“配方法”因式分解：x2+4xy-5y2

    (2) 若a+b=6, ab=5,求:①a2+b2, ②a4+b4的值

    （3）如果a2+2b2+c2-2ab-6b-4c+13=0，求a+b+c的值

    查看答案和解析>>

    科目：czsx 来源：2015-2016学年安徽六安舒城县晓天中学七年级下期中数学试卷（解析版） 题型：解答题

    阅读以下文字并解决问题：对于形如x2+2ax+a2这样的二次三项式，我们可以直接用公式法把它分解成（x+a）2的形式，但对于二次三项式x2+6x﹣27，就不能直接用公式法分解了．此时，我们可以在x2+6x﹣27中间先加上一项9，使它与x2+6x的和构成一个完全平方式，然后再减去9，则整个多项式的值不变． 即：x2+6x﹣27=（x2+6x+9）﹣9﹣27=（x+3）2﹣62=（x+3+6）（x+3﹣6）=（x+9）（x﹣3），像这样，把一个二次三项式变成含有完全平方式的形式的方法，叫做配方法．

    （1）利用“配方法”因式分【解析】
    x2+4xy﹣5y2

    （2）如果a2+2b2+c2﹣2ab﹣6b﹣4c+13=0，求a+b+c的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    （1）计算：数学公式．
    （2）请用指定的方法解下列方程：
    ①x2-9=0（用直接开平方法）；
    ②x2-6x=7（用配方法）；
    ③3x2-2=5x（用公式法）；
    ④x2+3x=10（用分解因式法）．

    查看答案和解析>>

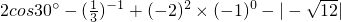    科目：czsx 来源：2010-2011学年四川省成都市金堂县九年级（上）期末数学试卷（解析版） 题型：解答题

    （1）计算：．
    （2）请用指定的方法解下列方程：
    ①x2-9=0（用直接开平方法）；
    ②x2-6x=7（用配方法）；
    ③3x2-2=5x（用公式法）；
    ④x2+3x=10（用分解因式法）．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （1）计算：2cos30°-(
    1
    3
    )-1+(-2)2×(-1)0-|-
    		12
    |    ．
    （2）请用指定的方法解下列方程：
    ①x2-9=0（用直接开平方法）；
    ②x2-6x=7（用配方法）；
    ③3x2-2=5x（用公式法）；
    ④x2+3x=10（用分解因式法）．

    查看答案和解析>>

    科目：czsx 来源：不详 题型：解答题

    （1）计算：2cos30°-(
    1
    3
    )-1+(-2)2×(-1)0-|-
    		12
    |    ．
    （2）请用指定的方法解下列方程：
    ①x2-9=0（用直接开平方法）；
    ②x2-6x=7（用配方法）；
    ③3x2-2=5x（用公式法）；
    ④x2+3x=10（用分解因式法）．

    查看答案和解析>>

    科目：czsx 来源： 题型：阅读理解

    认真阅读以下材料，并解答问题：
    （1）配方：利用完全平方公式，把二次三项式写成（a-k）2+h的形式．
    例：x2-2x=x2-2•1•x+12-12=（x-1）2-1
    （2）利用配方法解方程ax2+bx+c=0（a≠0）
    例：解方程x2-2x-3=0
    x2-2x=3
    x2-2•1•x+12=3+12
    （x-1）2=4
    x-1=±2
    ∴x1=3，x2=-1
    问题：（1）把多项式直接写成（a-k）2+h的形式：x2-6x-3=
    （x-3）2-12
    （x-3）2-12
    ．
    （2）用配方法解方程：x2+6x+8=0．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    认真阅读以下材料，并解答问题：
    （1）配方：利用完全平方公式，把二次三项式写成（a-k）2+h的形式．
    例：x2-2x=x2-2•1•x+12-12=（x-1）2-1
    （2）利用配方法解方程ax2+bx+c=0（a≠0）
    例：解方程x2-2x-3=0
    x2-2x=3
    x2-2•1•x+12=3+12
    （x-1）2=4
    x-1=±2
    ∴x1=3，x2=-1
    问题：（1）把多项式直接写成（a-k）2+h的形式：x2-6x-3=______．
    （2）用配方法解方程：x2+6x+8=0．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    5．认真阅读以下材料，并解答问题：
    材料：（1）配方：利用完全平方公式，把二次三项式写成（a-k）2+h的形式．
    例：x2-2x=x2-2•1•x+12-12=（x-1）2-1
    （2）利用配方法解方程ax2+bx+c=0（a≠0）
    问题：（1）把多项式直接写成（a-k）2+h的形式：x2-6x-3=（x-3）2-12
    （2）用配方法解方程：x2+6x+8=0．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    18．分解因式：x2+12x-189，分析：由于常数项数值较大，则将x2+12x变为完全平方公式，再运用平方差公式进行分解，这样简单易行：
    x2+12x-189=x2+2×6x+62-62-189
    =（x+6）2-36-189
    =（x+6）2-225
    =（x+6）2-152
    =（x+6+15）（x+6-15）
    =（x+21）（x-9）
    请按照上面的方法分解因式：x2-60x+884．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    小明同学把多项式（x2+6x+10）（x2+6x+8）+1分解因式的过程：
    设x2+6x=y，则
    原式=（y+10）（y+8）+1  （第一步）
    =y2+18y+81             （第二步）
    =（y+9）2              （第三步）
    =（x2+6x+9）2          （第四步）
    （1）该同学从第二步到第三步运用了因式分解的
     
    ．
    A．提取共因式法
    B．平方差公式
    C．两数和的完全平方公式
    D．两数差的完全平方公式
    （2）小明同学的因式分解是否彻底？若不彻底，请你直接写出因式分解的最后结果．
    （3）依据上题的解法尝试对（x2+4x-3）（x2+4x-7）+4进行因式分解．

    查看答案和解析>>