
科目:czsx 来源: 题型:
 如图,等腰梯形ABCD置于平面直角坐标系中,CD∥x轴,AB 在x轴上,AC平分∠DAB,直线AD的解析式为y=
如图,等腰梯形ABCD置于平面直角坐标系中,CD∥x轴,AB 在x轴上,AC平分∠DAB,直线AD的解析式为y=| 4 |
| 3 |
| 3 |
| 4 |
科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:解答题
 x-1>2x,并把解集在数轴上表示出来;
x-1>2x,并把解集在数轴上表示出来;
科目:czsx 来源: 题型:
| 3 | 2 |
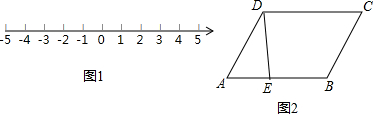
科目:czsx 来源: 题型:
 点E,交线段BC(或CD)于点F.
点E,交线段BC(或CD)于点F.| 3 |
| 3 |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
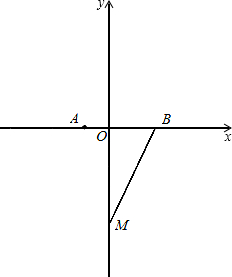 点M在y轴的负半轴上,且|AB|=6,cos∠OBM=
点M在y轴的负半轴上,且|AB|=6,cos∠OBM=
| ||
| 5 |
科目:czsx 来源: 题型:
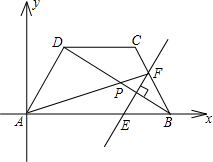
 如图,直线AB的函数解析式为y=x+2分别与x、y轴交于点A,点B,直线CD的函数解析为y=2x-1分别与x轴、y轴交于点C、点D,直线AB与CD相交于点P.
如图,直线AB的函数解析式为y=x+2分别与x、y轴交于点A,点B,直线CD的函数解析为y=2x-1分别与x轴、y轴交于点C、点D,直线AB与CD相交于点P.科目:czsx 来源: 题型:
| 3 |
| 4 |
| 9 |
| 4 |
 在实数m,使得△APQ与△AEC相似?如存在,请求出实数m的值;如不存在,请说明理由.
在实数m,使得△APQ与△AEC相似?如存在,请求出实数m的值;如不存在,请说明理由.科目:czsx 来源:2008年浙江省义乌市初中毕业升学统一考试、数学考试 题型:044
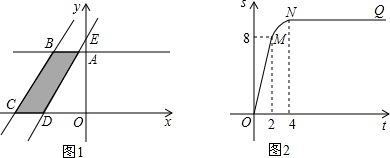
如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l.将直线l平移,平移后的直线l与x轴交于点D,与y轴交于点E.
(1)将直线l向右平移,设平移距离CD为t(t≥0),直角梯形OABC被直线l扫过的面积(图中阴影部份)为s,s关于t的函数图象如图2所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积;
②当2<t<4时,求S关于t的函数解析式;
(2)在第(1)题的条件下,当直线l向左或向右平移时(包括l与直线BC重合),在直线AB上是否存在点P,使△PDE为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
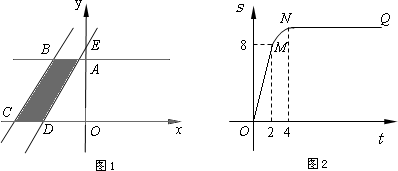
科目:czsx 来源: 题型:解答题
 点M在y轴的负半轴上,且|AB|=6,cos∠OBM=
点M在y轴的负半轴上,且|AB|=6,cos∠OBM=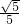 ,点C是M关于x轴的对称点.
,点C是M关于x轴的对称点.科目:czsx 来源: 题型:解答题
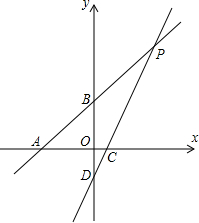 如图,直线AB的函数解析式为y=x+2分别与x、y轴交于点A,点B,直线CD的函数解析为y=2x-1分别与x轴、y轴交于点C、点D,直线AB与CD相交于点P.
如图,直线AB的函数解析式为y=x+2分别与x、y轴交于点A,点B,直线CD的函数解析为y=2x-1分别与x轴、y轴交于点C、点D,直线AB与CD相交于点P.科目:czsx 来源: 题型:解答题
 如图,在平面直角坐标系中,四边形ABCD是梯形,AB∥CD,点B(10,0),C(7,4).直线l经过A,D两点,且sin∠DAB=
如图,在平面直角坐标系中,四边形ABCD是梯形,AB∥CD,点B(10,0),C(7,4).直线l经过A,D两点,且sin∠DAB= .动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
.动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.科目:czsx 来源: 题型:
如图,在平面直角坐标系中,四边形ABCD是梯形,AB∥CD,点B(10,0),C(7,4).直线l经过A,D两点,且sin∠DAB=![]() .动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止
.动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止![]() 运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.

(1)点A的坐标为 ,直线l的解析式为 ;
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围;
(3)试求(2)中当t为何值时,S的值最大,并求出S的最大值;
(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
科目:czsx 来源:2012届浙江省丽水市中考模拟试卷2数学试卷(带解析) 题型:解答题
如图1,在平面直角坐标系xOy中,点A,B坐标分别为(8,4),(0,4),线段CD在于x轴上,CD=3,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E,交OA于点G,连结CE交OA于点F. 设运动时间为t,当E点到达A点时,停止所有运动.
(1)求线段CE的长;
(2)记S为RtΔCDE与ΔABO的重叠部分面积,试写出S关于t函数关系式及t的取值范围;
(3)如图2,连结DF,
1当t取何值时,以C,F,D为顶点的三角形为等腰三角形?
2直接写出ΔCDF的外接圆与OA相切时t的值.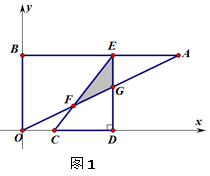

科目:czsx 来源:第2章《二次函数》中考题集(38):2.7 最大面积是多少(解析版) 题型:解答题
 x-2
x-2 ,求m的值;
,求m的值;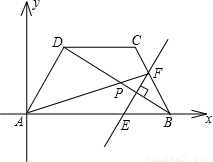
科目:czsx 来源:第34章《二次函数》中考题集(42):34.4 二次函数的应用(解析版) 题型:解答题
 x-2
x-2 ,求m的值;
,求m的值;
科目:czsx 来源:第2章《二次函数》中考题集(41):2.3 二次函数的应用(解析版) 题型:解答题
 x-2
x-2 ,求m的值;
,求m的值;
科目:czsx 来源:第6章《二次函数》中考题集(41):6.4 二次函数的应用(解析版) 题型:解答题
 x-2
x-2 ,求m的值;
,求m的值;