
科目:czsx 来源: 题型:
| 2 |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| k | x |
科目:czsx 来源: 题型:
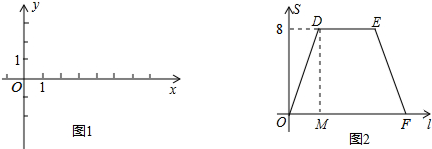
| 5 |
| 5 |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
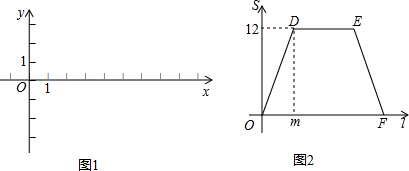
| 13 |
| 13 |
科目:czsx 来源: 题型:
| 4 |
| 5 |
 数y=
数y=| k |
| x |
| k |
| x |
| k |
| x |
科目:czsx 来源:中学学习一本通 数学 九年级下册 北师大课标 题型:044
| |||||||||||||||
科目:czsx 来源: 题型:解答题
 (k≠0)的图象与一次函数y=x+b的图象交于A(-1,b-1)、B(-5,b-5)两点.
(k≠0)的图象与一次函数y=x+b的图象交于A(-1,b-1)、B(-5,b-5)两点.科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:解答题
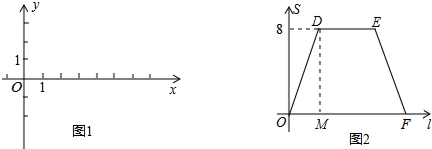
科目:czsx 来源: 题型:解答题
 时,求直线AB的解析式.
时,求直线AB的解析式.科目:czsx 来源: 题型:解答题
 ,若反比例函
,若反比例函 数y=
数y= (x>0)的图象恰好过点A.
(x>0)的图象恰好过点A. (x>0)的解析式.
(x>0)的解析式. (x>0)的图象上?并说明理由.
(x>0)的图象上?并说明理由.科目:czsx 来源: 题型:解答题
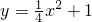 上的一个动点.
上的一个动点.
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
已知:在如图1所示的平面直角坐标系xOy中,A,C两点的坐标分别为![]() ,
,
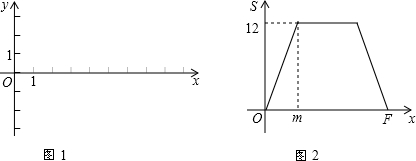
![]() (其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O—A—B—C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.
(其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O—A—B—C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.
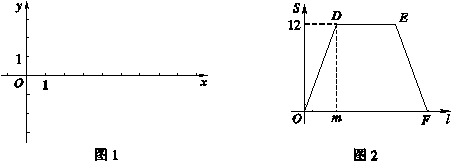
1.(1)结合以上信息及图2填空:图2中的m= ;
2.(2)求B,C两点的坐标及图2中OF的长;
3.(3)在图1中,当动点P恰为经过O,B两点的抛物线W的顶点时,
①求此抛物线W的解析式;
② 若点Q在直线![]() 上方的抛物线W上,坐标平面内另有一点R,满足以B,
上方的抛物线W上,坐标平面内另有一点R,满足以B,
P,Q,R四点为顶点的四边形是菱形,求点Q的坐标.
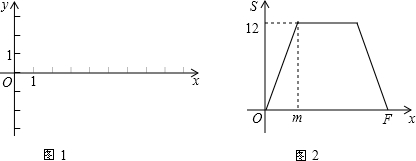
科目:czsx 来源: 题型:
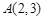 ,
,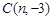 (其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O—A—B—C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.
(其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O—A—B—C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.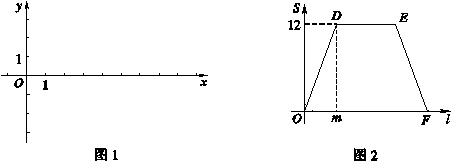
 图2中OF的长;
图2中OF的长;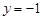 上方的抛物线W上,坐标平面内另有一点R,满足以B,
上方的抛物线W上,坐标平面内另有一点R,满足以B,科目:czsx 来源:2011-2012学年北京市西城区九年级第一学期期末测试数学卷 题型:解答题
已知:在如图1所示的平面直角坐标系xOy中,A,C两点的坐标分别为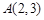 ,
,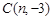 (其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O—A—B—C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.
(其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O—A—B—C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.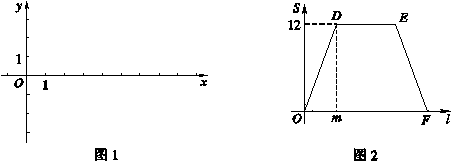
【小题1】(1)结合以上信息及图2填空:图2中的m= ;
【小题2】(2)求B,C两点的坐标及 图2中OF的长;
图2中OF的长;
【小题3】(3)在图1中,当动点P恰为经过O,B两点的抛物线W的顶点时,
① 求此抛物线W的解析式;
② 若点Q在直线 上方的抛物线W上,坐标平面内另有一点R,满足以B,
上方的抛物线W上,坐标平面内另有一点R,满足以B,
P,Q,R四点为顶点的四边形是菱形,求点Q的坐标.