
科目:czsx 来源:2015-2016学年江苏省无锡市北塘区八年级上学期期中考试数学试卷(解析版) 题型:解答题
已知:如图,BC//EF,AD=BE,BC=EF.求证:△ABC≌△DEF.

科目:czsx 来源: 题型:解答题
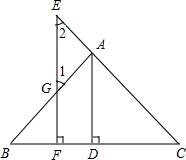 已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.
已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:解答题

科目:czsx 来源:2015-2016学年江苏省镇江市八年级上学期期中考试数学试卷(解析版) 题型:解答题
已知:如图,BC//EF,AD=BE, BC=EF,求证:

(1)△ABC≌△DEF.
(2)AC//DF
科目:czsx 来源:2012-2013学年江苏泰州高港实验学校八年级上学期期中考试数学试卷(带解析) 题型:解答题
已知矩形ABCD,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.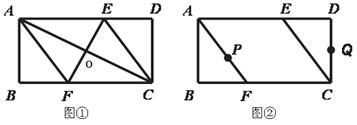
(1)如图①,连接AF、CE,求证四边形AFCE是菱形;
(2)求AF的长;
(3)如图②,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自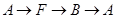 停止,点Q自
停止,点Q自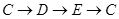 停止,在运动过程中:已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动的时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
停止,在运动过程中:已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动的时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
科目:czsx 来源:2012-2013学年江苏泰州高港实验学校八年级上学期期中考试数学试卷(解析版) 题型:解答题
已知矩形ABCD,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.

(1)如图①,连接AF、CE,求证四边形AFCE是菱形;
(2)求AF的长;
(3)如图②,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自 停止,点Q自
停止,点Q自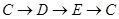 停止,在运动过程中:已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动的时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
停止,在运动过程中:已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动的时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
科目:czsx 来源: 题型:
已知矩形ABCD,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图①,连接AF、CE,求证四边形AFCE是菱形.
(2)求AF的长.
(3)如图②,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自![]() 停止,点Q自
停止,点Q自![]() 停止,在
停止,在![]() 运动过程中:
运动过程中:
已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动的时间为t秒,当A、C、P、Q四点为顶点的四边形是平行![]() 四边形时,求t的值.
四边形时,求t的值.

科目:czsx 来源: 题型:
| DE |
| BD |
| 1 |
| 2 |
| 17 |
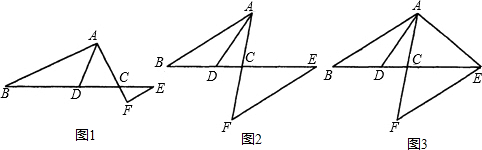
科目:czsx 来源: 题型:
| DE |
| BD |
| DE |
| BD |

科目:czsx 来源: 题型:解答题
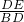 =k,过E作EF∥AB交AC的延长线于F.
=k,过E作EF∥AB交AC的延长线于F. ,AE=2
,AE=2 ,且AF>EF,求边AC的长.
,且AF>EF,求边AC的长.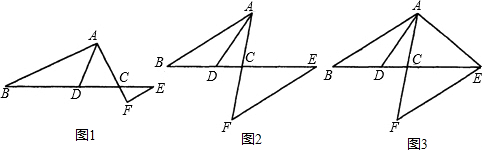
科目:czsx 来源:2013年四川省眉山市仁寿县彰加镇中中考数学模拟试卷(解析版) 题型:解答题
 ,过E作EF∥AB交AC的延长线于F.
,过E作EF∥AB交AC的延长线于F.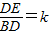 时,请猜想线段AF、EF、AB之间满足的数量关系(含k),并证明你的结论.
时,请猜想线段AF、EF、AB之间满足的数量关系(含k),并证明你的结论.
科目:czsx 来源:2010年黑龙江省哈尔滨市南岗区中考数学一模试卷(解析版) 题型:解答题
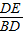 =k,过E作EF∥AB交AC的延长线于F.
=k,过E作EF∥AB交AC的延长线于F. ,AE=2
,AE=2 ,且AF>EF,求边AC的长.
,且AF>EF,求边AC的长.
科目:czsx 来源: 题型:
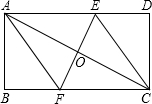 已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.