

分析 (1)当t=0时,根据正方形的判定和性质,进而利用全等三角形的判定和性质解答即可;
(2)根据等腰直角三角形的性质和三角形的面积公式进行解答即可;
(3)根据平行四边形的判定和性质解答即可.
解答 解:(1)当t=0时,可得点N与点A重合,连接DE,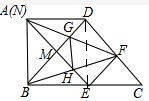
∵AD=AB,∠DAB=90°,
∴∠ABD=45°,
∵AM⊥BD,
∴∠BAE=45°,
∵∠ABC=90°,
∴BE=AB,
∴四边形ABED是正方形,
∴DE⊥BC,
∵BE=$\frac{1}{2}$BC,
∴BD=DC,
∴∠C=45°,
∴∠CDE=45°,∠BDC=90°,
∵EF⊥CD,
∴DF=EF,∠DEF=∠EDF=45°,
∴∠ADE+∠EDF=∠BED+∠DEF,即∠ADF=∠BEF,
∵AD=BE,
在△ADF与△BEF中,
$\left\{\begin{array}{l}{AD=BE}\\{∠ADF=∠BEF}\\{DF=EF}\end{array}\right.$,
∴△ADF≌△BEF,
∴∠AFD=∠BFE,易得∠HEF=90°,
∵DF=EF,∠CDB=∠HEF=90°,△FDG≌△FEH,
∴GF=HF;
(2)因为△NBE与△EFC是等腰直角三角形,∠NEF=90°,
∵S△NEF=$\frac{1}{2}$NE•EF,由题意可知:AN=tcm,
∴BE=BN=(4-t)cm,NE=$\sqrt{2}(4-t)$cm,EC=BC-BE=(4+t)cm,
∴EF=$\frac{4+t}{\sqrt{2}}$cm,
∴${S}_{△NEF}=\frac{1}{2}NE•EF=\frac{1}{2}×\sqrt{2}(4-t)•\frac{4+t}{\sqrt{2}}=6$,
解得:t=-2(舍去)或t=2,
∴当t=2时,△NEF的面积为6cm2,;
(3)当GE=BE时,
∵NE⊥BD,
∴BM=GM,
∵BE=BN,
∴NM=ME,
∴四边形BEGN是平行四边形,
∴NF∥BC,
∵∠FEC=45°,
∴∠NFE=45°,
∴NE=EF,即$\sqrt{2}(4-t)=\frac{4+t}{\sqrt{2}}$,
解得:t=$\frac{4}{3}$,
∴当t为$\frac{4}{3}$时,GE=BE,此时NF与BC的位置关系是平行.
点评 本题考查了四边形综合题,关键是根据平行四边形的判定和性质,等腰直角三角形的运用解答,并且根据等腰直角三角形的性质和三角形的面积公式进行解答.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
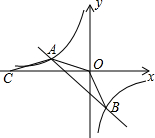 如图,直线AB与反比例函数的图象交于A(-4,m)、B(2,n)两点,点C在x轴上,AO=AC,△OAC的面积为8.
如图,直线AB与反比例函数的图象交于A(-4,m)、B(2,n)两点,点C在x轴上,AO=AC,△OAC的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
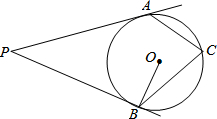 如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )
如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )| A. | 50° | B. | 60° | C. | 65° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3-2$\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | 1-$\sqrt{2}$ | D. | 3+2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
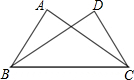 如图,已知∠ABC=∠DCB,下列所给条件①∠A=∠D;②AB=DC;③∠ACB=∠DBC;④AC=DB.其中能证明△ABC≌△DCB的条件是①②③(把所有正确条件的序号都选上)
如图,已知∠ABC=∠DCB,下列所给条件①∠A=∠D;②AB=DC;③∠ACB=∠DBC;④AC=DB.其中能证明△ABC≌△DCB的条件是①②③(把所有正确条件的序号都选上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com