
科目:czsx 来源:黄冈难点课课练 七年级数学下册(北师大版) 题型:044
如图所示,△ABC、△ECD都是等腰直角三角形,且点C在AD上,AE的延长线与BD交于F.请你在图中找出一对全等三角形,并写出证明它们全等的过程.

科目:czsx 来源:解题升级解题快速反应一典通八年级数学 题型:044
如图所示,正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=![]() AB.(1)求证:△ABE≌△ADF.
AB.(1)求证:△ABE≌△ADF.

(2)阅读下列材料:
如图所示,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置;

如图所示,以BC为轴把△ABC翻折![]() ,可以变到△DBC的位置;
,可以变到△DBC的位置;

如图所示,以点A为中心,把△ABC旋转![]() ,可以变到△AED的位置.
,可以变到△AED的位置.

像这样,其中一个三角形由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换叫做三角形的全等变换.
回答下列问题:
①如图所示,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置?答:________.

②指出图中线段BE与DF之间的关系.答:________.

科目:czsx 来源:同步题 题型:解答题
 。
。 
科目:czsx 来源:课堂三级讲练数学九年级(上) 题型:044
阅读下列问题再解答:如图所示,AB是⊙O直径,CD是弦且CD⊥AB,点E是![]() 中点,连CE,DE则DE∥AB,若D点、B点、A点不动,C点在
中点,连CE,DE则DE∥AB,若D点、B点、A点不动,C点在![]() 运动使∠ECD不变,那么DE与AB还平行吗?结论是平行的.
运动使∠ECD不变,那么DE与AB还平行吗?结论是平行的.
理由:C点在不断运动中∠ECD不变,即![]() =
=![]() ,如图(2),∵∠DCE=∠ECB,E是
,如图(2),∵∠DCE=∠ECB,E是![]() 中点,∴AB∥DE.
中点,∴AB∥DE.

问题:如图,⊙O直径AB=8,D是半圆(A,B除外)上任一点,∠ADB的平分线交⊙O于C,弦EF过AC,BC的中点M,N.(1)不论D怎么运动,△ABC是一个怎样特殊三角形;(2)求EF的长.

科目:czsx 来源:山东省期末题 题型:解答题

科目:czsx 来源: 题型:解答题
 探究题
探究题科目:czsx 来源: 题型:
 26、探究题
26、探究题科目:czsx 来源:2012年苏教版初中数学七年级下 11.2全等三角形练习卷(解析版) 题型:解答题
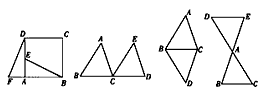
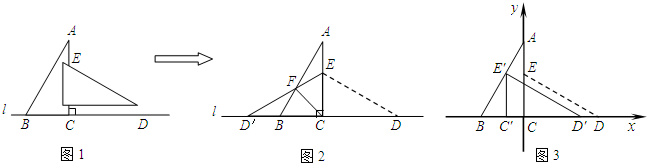
阅读下列材料:
如图(1)所示,把△ABC沿直线BC移动线段BC那样长的距离可以变到△ECD的位置;
如图(2)所示,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;
如图(3)所示,以点A为中心,把△ABC旋转180°,可以变到△AED的位置.
像这样,只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换. 在全等变换中可以清楚地识别全等三角形的对应元素,以上的三种全等变换分别叫平移变换、翻折变换和旋转变换.
问题:如图(4),△ABC≌△DEF,B和E、C和F是对应顶点,问通过怎样的全等变换可以使它们重合,并指出它们相等的边和角.
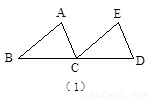

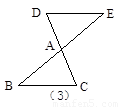
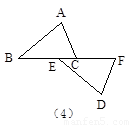
科目:czsx 来源:2012年人教版八年级上第十一章全等三角形第一节全等三角形练习卷(解析版) 题型:解答题
(阅读与探究)如图(1)所示,把△ABC沿直线BC移动线段BC那样长的距离可以变到△ECD的位置;如图(2)所示,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;如图(3)所示,以点A为中心,把△ABC旋转180°,可以变到△AED的位置,像这样,只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换. 在全等变换中可以清楚地识别全等三角形的对应元素,以上的三种全等变换分别叫平移变换、翻折变换和旋转变换.
问题:如图(4),△ABC≌△DEF,B和E、C和F是对应顶点,问通过怎样的全等变换可以使它们重合,并指出它们相等的边和角.




科目:czsx 来源: 题型:阅读理解
(阅读与探究)如图(1)所示,把△ABC沿直线BC移动线段BC那样长的距离可以变到△ECD的位置;如图(2)所示,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;如图(3)所示,以点A为中心,把△ABC旋转180°,可以变到△AED的位置,像这样,只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换. 在全等变换中可以清楚地识别全等三角形的对应元素,以上的三种全等变换分别叫平移变换、翻折变换和旋转变换.
问题:如图(4),△ABC≌△DEF,B和E、C和F是对应顶点,问通过怎样的全等变换可以使它们重合,并指出它们相等的边和角.




科目:czsx 来源: 题型:
| 1 |
| 2 |

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
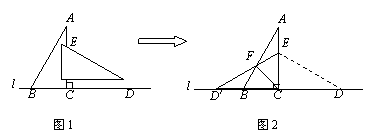
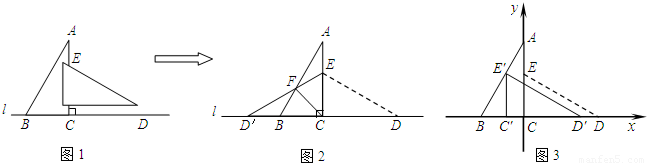
将两块形状大小完全相同的直角三角板按如图1所示的方式拼在一起。它们中较![]() 小直角边的长为6cm,较小锐角的度数为30°.(1)将△ECD沿直线AC翻折到如图2的位置,连接CF,图中除了△ABC≌△ECD≌△ECD′外,还有没有全等的三角形?若有,请指出一对并给出证明。
小直角边的长为6cm,较小锐角的度数为30°.(1)将△ECD沿直线AC翻折到如图2的位置,连接CF,图中除了△ABC≌△ECD≌△ECD′外,还有没有全等的三角形?若有,请指出一对并给出证明。
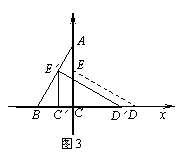
 |
(2)以点C为坐标原点建立如图3所示的直角坐标系,将△ECD沿x轴向左平移,使E点落在AB上,请求出点E′的坐标。
科目:czsx 来源:2013年山东省济南市中考数学模拟试卷(十八)(解析版) 题型:解答题
科目:czsx 来源:2013年四川省眉山市仁寿县汪洋镇中中考数学模拟试卷(解析版) 题型:解答题
