
科目:czsx 来源: 题型:解答题
在平面直角坐标系中, 抛物线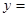
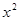 +
+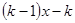 与直线
与直线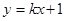 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.
(1)如图1,当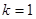 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线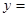
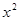 +
+ 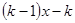
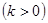 与
与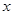 轴交于C,D两点(点C在点D的左侧).在直线
轴交于C,D两点(点C在点D的左侧).在直线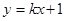 上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时
上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时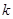 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.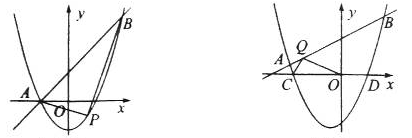
图1 图2
科目:czsx 来源:不详 题型:解答题

 +
+ 与直线
与直线 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧. 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标;
 +
+ 
 与
与 轴交于C,D两点(点C在点D的左侧).在直线
轴交于C,D两点(点C在点D的左侧).在直线 上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时
上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:czsx 来源:2014年初中毕业升学考试(广西南宁卷)数学(解析版) 题型:解答题
在平面直角坐标系中, 抛物线
 +
+ 与直线
与直线 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.
(1)如图1,当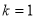 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线
 +
+ 
 与
与 轴交于C,D两点(点C在点D的左侧).在直线
轴交于C,D两点(点C在点D的左侧).在直线 上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时
上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

图1 图2
科目:czsx 来源: 题型:
在平面直角坐标系中, 抛物线
 +
+ 与直线
与直线 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.
(1) 如图 ,当
,当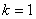 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标;
(2) 在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3) 如图 ,抛物线
,抛物线
 +
+ 
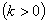 与
与 轴交于C,D两点(点C在点D的左侧).在直线
轴交于C,D两点(点C在点D的左侧).在直线 上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时
上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.



科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
 如图在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点A坐标为(0,-2),点B在抛物线y=ax2+ax-2上.
如图在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点A坐标为(0,-2),点B在抛物线y=ax2+ax-2上.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:czsx 来源: 题型:
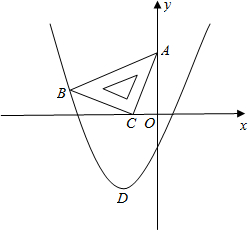 如图在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示点B在抛物线y=ax2+ax-2上.
如图在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示点B在抛物线y=ax2+ax-2上.科目:czsx 来源: 题型:解答题
 如图在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示点B在抛物线y=ax2+ax-2上.
如图在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示点B在抛物线y=ax2+ax-2上.科目:czsx 来源: 题型:解答题
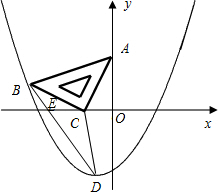 如图在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点A坐标为(0,-2),点B在抛物线y=ax2+ax-2上.
如图在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点A坐标为(0,-2),点B在抛物线y=ax2+ax-2上.科目:czsx 来源: 题型:
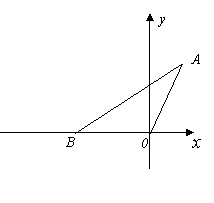
如图在平面直角坐标系中,点A的坐标为(1,![]() ) ,△AOB的面积是
) ,△AOB的面积是![]() .
.
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(4)在(2)中![]() 轴下方的抛物线上是否存在一点P,过点P作
轴下方的抛物线上是否存在一点P,过点P作![]() 轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
 |
科目:czsx 来源: 题型:
如图,在平面直角坐标系中,A(-3,0),点C在y轴的正半轴上,BC∥x轴,且BC=5,AB交y轴于点D,OD=![]() .
.

(1)求出点C的坐标;
(2)过A、C、B三点的抛物线与x轴交于点E,连接BE.若动点M从点A出发沿x轴向x轴正方向运动,同时动点N从点E出发,在直线EB上作匀速运动,两个动点的运动速度均为每秒1个单位长度,请问当运动时间t为多少秒时,△MON为直角三角形?
科目:czsx 来源: 题型:
 .
.
科目:czsx 来源:2011年广东省徐闻县第一中学初二第一学期期末考试数学卷 题型:解答题
如图,在平面直角坐标系中,A(-3,0),点C在y轴的正半轴上,BC∥x轴,且BC=5,AB交y轴于点D,OD=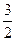 .
.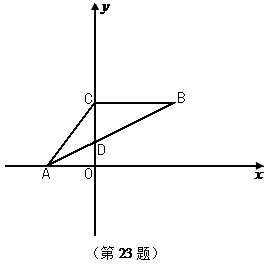
(1)求出点C的坐标;
(2)过A、C、B三点的抛物线与x轴交于点E,连接BE.若动点M从点A出发沿x轴向x轴正方向运动,同时动点N从点E出发,在直线EB上作匀速运动,两个动点的运动速度均为每秒1个单位长度,请问当运动时间t为多少秒时,△MON为直角三角形?
科目:czsx 来源:2013-2014学年山东烟台海阳市九年级上期末数学试卷(解析版) 题型:解答题
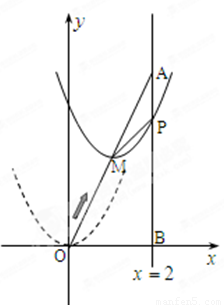
如图,在平面直角坐标系中,已知点 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与 轴相交于点
轴相交于点 ,连结
,连结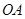 ,抛物线y=x
,抛物线y=x
 从点
从点 沿
沿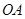 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点 ,顶点
,顶点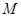 到
到 点时停止移动.
点时停止移动.
(1)求线段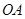 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点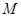 的横坐标为
的横坐标为 ,
,
①用 的代数式表示点
的代数式表示点 的坐标;
的坐标;
②当 为何值时,线段
为何值时,线段 最短;
最短;
(3)当线段 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点 ,使△
,使△ 的面积与△
的面积与△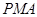 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
科目:czsx 来源:2012年宁夏银川市景博中学中考数学一模试卷(解析版) 题型:解答题

科目:czsx 来源:2011年广东省初二第一学期期末考试数学卷 题型:解答题
如图,在平面直角坐标系中,A(-3,0),点C在y轴的正半轴上,BC∥x轴,且BC=5,AB交y轴于点D,OD= .
.
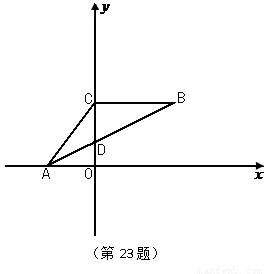
(1)求出点C的坐标;
(2)过A、C、B三点的抛物线与x轴交于点E,连接BE.若动点M从点A出发沿x轴向x轴正方向运动,同时动点N从点E出发,在直线EB上作匀速运动,两个动点的运动速度均为每秒1个单位长度,请问当运动时间t为多少秒时,△MON为直角三角形?
科目:czsx 来源: 题型:解答题
如图,在平面直角坐标系中,已知点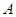 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与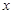 轴相交于点
轴相交于点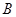 ,连结
,连结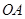 ,抛物线y=x
,抛物线y=x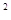
 从点
从点 沿
沿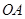 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点 ,顶点
,顶点 到
到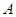 点时停止移动.
点时停止移动.
(1)求线段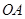 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点 的横坐标为
的横坐标为 ,
,
①用 的代数式表示点
的代数式表示点 的坐标;
的坐标;
②当 为何值时,线段
为何值时,线段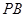 最短;
最短;
(3)当线段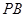 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点 ,使△
,使△ 的面积与△
的面积与△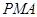 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
科目:czsx 来源:不详 题型:解答题
 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与 轴相交于点
轴相交于点 ,连结
,连结 ,抛物线y=x
,抛物线y=x
 从点
从点 沿
沿 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点 ,顶点
,顶点 到
到 点时停止移动.
点时停止移动.
 所在直线的函数解析式;
所在直线的函数解析式; 的横坐标为
的横坐标为 ,
, 的代数式表示点
的代数式表示点 的坐标;
的坐标; 为何值时,线段
为何值时,线段 最短;
最短; 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点 ,使△
,使△ 的面积与△
的面积与△ 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.科目:czsx 来源:不详 题型:解答题

科目:czsx 来源:不详 题型:解答题
 .
.