科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:解答题
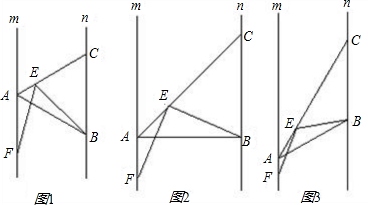
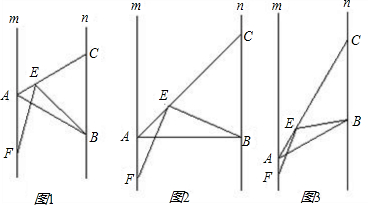
 如图,已知∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠MAE=∠NAF;②BE=CF;③△ACN≌△ABM;④CD=DN.
如图,已知∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠MAE=∠NAF;②BE=CF;③△ACN≌△ABM;④CD=DN.科目:czsx 来源:2007-2008学年广东省深圳市学府中学九年级(上)第一次月考数学试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:
 20、如图,已知∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠MAE=∠NAF;②BE=CF;③△ACN≌△ABM;④CD=DN.
20、如图,已知∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠MAE=∠NAF;②BE=CF;③△ACN≌△ABM;④CD=DN.科目:czsx 来源: 题型:
 如图所示,已知∠E=∠F=90°,∠B=∠C,AE=AF,则以下结论有哪些是成立的?并挑选一个将理由补充完整:
如图所示,已知∠E=∠F=90°,∠B=∠C,AE=AF,则以下结论有哪些是成立的?并挑选一个将理由补充完整:科目:czsx 来源: 题型:
 交于另一点E.
交于另一点E.科目:czsx 来源: 题型:
| 3 |
科目:czsx 来源: 题型:
 ,交AD于F.
,交AD于F.| 1 |
| 2 |
| CE |
| AE |
| AF |
| DF |
| 4 |
| 5 |
| AF |
| DF |
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
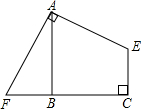 已知如图所示:四边形AECF中AE=AF,∠EAF=9O°,∠C=90°,AB⊥FC于B,且AB=BC,若FC=10,EC=6,求四边形AECF的面积.
已知如图所示:四边形AECF中AE=AF,∠EAF=9O°,∠C=90°,AB⊥FC于B,且AB=BC,若FC=10,EC=6,求四边形AECF的面积.科目:czsx 来源: 题型:
 已知E为正方形ABCD对角线AC上一点(不与A,C重合),将△BCE逆时针旋转可得到△BAF,连接EF.
已知E为正方形ABCD对角线AC上一点(不与A,C重合),将△BCE逆时针旋转可得到△BAF,连接EF.科目:czsx 来源: 题型:
 已知在正方形ABCD中,对角线AC、DB交于点O,E是CD边上一点,AE与对角线DB交于点M,连接CM.
已知在正方形ABCD中,对角线AC、DB交于点O,E是CD边上一点,AE与对角线DB交于点M,连接CM.| α-β |
| 2 |
| α-β |
| 2 |
科目:czsx 来源:浙江省宁波五校2012届九年级下学期第一次联考数学试题 题型:013
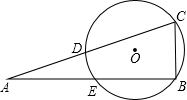
已知:如图,Rt△ABC外切于⊙O,切点分别为E、F、H,∠ABC=90°,直线FE、CB交于D点,连结AO、HE,则下列结论:
①∠FEH=45°+∠FAO
②BD=AF
③AB2=AO×DF
④AE×CH=S△ABC

其中正确的是
A.①②③④
B.①③④
C.②③④
D.①②③
科目:czsx 来源:2013年重庆市高级中等学校招生考试数学B卷 题型:044
已知,在矩形ABCD中,E为BC边上一点,AE⊥DE,AB=12,BE=16,F为线段BE上一点,EF=7,连接AF.图1,现有一张硬质纸片△GMN,∠NGM=90°,NG=6,MG=8,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上.图2,△GMN从图1的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点出发,以每秒1个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ.当点N到达终点B时,△GMN和点P同时停止运动.设运动时间为t秒,解答下列问题:

(1)在整个运动过程中,当点G在线段AE上时,求t的值;
(2)在整个运动过程中,是否存在点P,使△APQ是等腰三角形,若存在,求出t的值;若不存在,说明理由;
(3)在整个运动过程中,设△GMN与△AEF重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围.
科目:czsx 来源: 题型:单选题
 已知:如图,Rt△ABC外切于⊙O,切点分别为E、F、H,∠ABC=90°,直线FE、CB交于D点,连接AO、HE,则下列结论:
已知:如图,Rt△ABC外切于⊙O,切点分别为E、F、H,∠ABC=90°,直线FE、CB交于D点,连接AO、HE,则下列结论:科目:czsx 来源: 题型:单选题
科目:czsx 来源: 题型:解答题
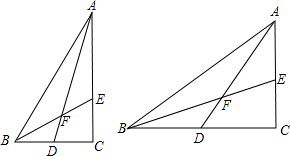
 已知:如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC.
已知:如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC.科目:czsx 来源: 题型:解答题
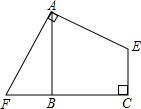 已知如图所示:四边形AECF中AE=AF,∠EAF=9O°,∠C=90°,AB⊥FC于B,且AB=BC,若FC=10,EC=6,求四边形AECF的面积.
已知如图所示:四边形AECF中AE=AF,∠EAF=9O°,∠C=90°,AB⊥FC于B,且AB=BC,若FC=10,EC=6,求四边形AECF的面积.科目:czsx 来源: 题型:解答题
 ,AF=1,求EM的长.
,AF=1,求EM的长.