如图.在□abcd中.e是ad上的一点.连接be.f为be中点答案解析
科目:czsx
来源:
题型:
如图,E、F是平行四边形对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.判定平行四边形的方法很多,在具体应用时,到底 用哪种方法更好呢?
用哪种方法更好呢?
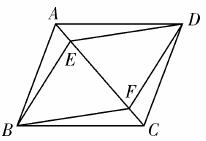
小明、小华、小 颖三位同学对此题进行探讨,给出了各自不同的证明如下:
颖三位同学对此题进行探讨,给出了各自不同的证明如下:
小明的证明方法:
∵ 四边形ABCD是平行四边形,
∴ AD∥BC,AD=BC.
∴ ∠DAE=∠BCF.
又 AE=CF,
∴ △AED≌△CFB.
∴ DE=BF,∠AED=∠CFB.
∴ ∠DEF=∠BFE.
∴  ED∥BF.
ED∥BF.
∴ 四边形BEDF是平行四边形.
小华的证明方法:
∵ 四边形ABCD是平行四边形,
∴ AD∥BC,AD=BC.
∴ ∠DAE=∠BCF.
又 AE=CF,
∴ △AED≌△CF B.
B.
∴ DE=BF.
同理可证△ABE≌△CDF.
∴ BE=DF.
∴ 四边形BEDF是平行四边形.
小颖的证明方法:
如图,连接BD交AC于点O.

∵ 四边形ABCD是平行四边形,
∴ AO=OC,BO=OD.
又 AE=CF,
∴ OE=OF.
由BO=OD,OE=OF知四边形BEDF是平行四边形.
就这三名同学的证明方法 ,你认为哪一种方法最为简捷?从中你得到什么启示?
,你认为哪一种方法最为简捷?从中你得到什么启示?
查看答案和解析>>
科目:czsx
来源:
题型:解答题
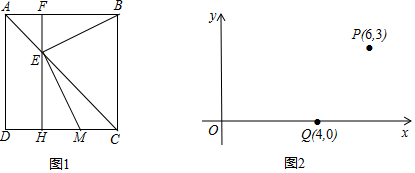
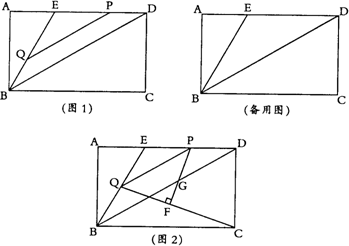
17.如图1,点E是正方形ABCD的对角线AC上一动点,连接BE,过E作ME⊥EB交DC于点M.
(1)求证:BE=ME.
小明给出的思路为:过E作AD的平分线,分别交AB、DC于F、H,请完善小明的证明过程.
(2)若正方形ABCD的边长为4,当DM=3时,求AE的长度?
(3)探索,如图2,在直角坐标系中,点P坐标(6,3),点Q坐标(4,0),在直角坐标系中找一点G,使得△PQG为等腰直角三角形,且∠PGQ=90°,直接写出点G的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
3.小明遇到这样一个问题,如图1,△ABC中,AB=7,AC=5,点D为BC的中点,求AD的取值范围.
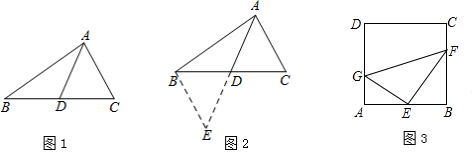
小明发现老师讲过的“倍长中线法”可以解决这个问题,所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,他的做法是:如图2,延长AD到E,使DE=AD,连接BE,构造△BED≌△CAD,经过推理和计算使问题得到解决.
请回答:(1)小明证明△BED≌△CAD用到的判定定理是:SAS(用字母表示)
(2)AD的取值范围是1<AD<6
小明还发现:倍长中线法最重要的一点就是延长中线一倍,完成全等三角形模型的构造.
参考小明思考问题的方法,解决问题:
如图3,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若AG=2,BF=4,∠GEF=90°,求GF的长.
查看答案和解析>>
科目:czsx
来源:2015届广西桂林市灌阳县八年级上学期期中测试数学试卷(解析版)
题型:解答题
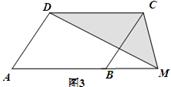
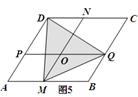
探究:已知平行四边形ABCD的面积为100,M是AB所在直线上的一点
(1)如图1:当点M与B重合时,S△DCM =________;

(2)如图2:当点M与B与A均不重合时,S△DCM =________
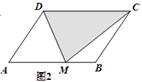
(3)如图3:当点M在AB(或BA)的延长线上时,S△DCM =________
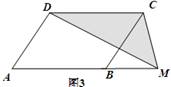
推广:平行四边形ABCD的面积为a,E、F为两边DC、BC延长线上两点,连接DF、AF、AE、BE.求出图4中阴影部分的面积,并简要说明理由
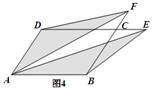
应用:如图5是某广场的一平行四边形绿地ABCD,PQ、MN分别平行DC、AD,PQ、MN交于O点,其中S四边形AM OP=300m2,S四边形MBQO=400m2,S四边形NCQO=700m2.现进行绿地改造,在绿地内部做一个三角形区域MQD,连接DM、QD、QM,(图中阴影部分)种植不同的花草,求三角形DMQ区域的面积.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
探究:已知平行四边形ABCD的面积为100,M是AB所在直线上的一点
(1)如图1:当点M与B重合时,S
△DCM =________;

(2)如图2:当点M与B与A均不重合时,S
△DCM =________
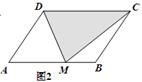
(3)如图3:当点M在AB(或BA)的延长线上时,S
△DCM =________
推广:平行四边形ABCD的面积为a,E、F为两边DC、BC延长线上两点,连接DF、AF、AE、BE.求出图4中阴影部分的面积,并简要说明理由

应用:如图5是某广场的一平行四边形绿地ABCD,PQ、MN分别平行DC、AD,PQ、MN交于O点,其中S
四边形AM OP=300m
2,S
四边形MBQO=400m
2,S
四边形NCQO=700m
2.现进行绿地改造,在绿地内部做一个三角形区域MQD,连接DM、QD、QM,(图中阴影部分)种植不同的花草,求三角形DMQ区域的面积.
查看答案和解析>>
科目:czsx
来源:
题型:

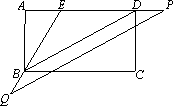
如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA.
(1)判断△APB是什么三角形,证明你的结论;
(2)比较DP与PC的大小;
(3)画出以AB为直径的⊙O,交AD于点E,连接BE与AP交于点F,若tan∠BPC=
,求tan∠AFE的值.
查看答案和解析>>
科目:czsx
来源:
题型:
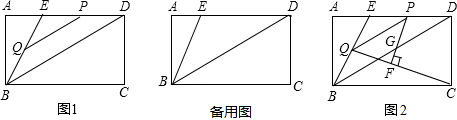
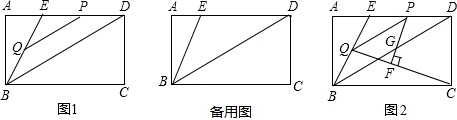
在矩形ABCD中,点E是AD边上一点,连接BE,且∠ABE=30°,BE=DE,连接BD.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.
(1)当点P在线段ED上时(如图1),求证:BE=PD+
PQ;
(2)若BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与x的函数关系式(不要求写出自变量x的取值范围);
(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PG的长.
查看答案和解析>>
科目:czsx
来源:
题型:
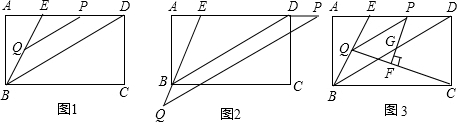
在矩形ABCD中,点E是AD边上一点,连接BE,且BE=2AE,BD是∠EBC的平分线.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.
(1)当点P在线段ED上时(如图1),求证:BE=PD+
PQ;
(2)当点P在线段ED的延长线上时(如图2),请你猜想BE,PD,
PQ三者之间的数量关系(直接写出结果,不需说明理由);
(3)当点P运动到线段ED的中点时(如图3),连接QC,过点P作PF⊥QC,垂足为F,PF交BD于点G.若BC=12,求线段PG的长.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA,若AD=50mm,AP=80mm.
(1)判断△APB是什么三角形,证明你的结论;
(2)比较DP与PC的大小;
(3)画出以AB为直径的⊙O,交AD于点E,连接BE与AP交于点F,求tan∠AFE的值;
(4)点O′在线段AB上移动,以O’为圆心作⊙O′,使⊙O′与边AP相切,切点为M,设⊙O′的半径为m,当m为何值时,⊙O′与AP、BF都相切?
查看答案和解析>>
科目:czsx
来源:2009年北京市门头沟区初三二模数学试题
题型:044
在矩形ABCD中,点E是AD边上一点,连结BE,且BE=2AE,BD是∠EBC的平分线.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.
(1)当点P在线段ED上时(如图),求证: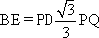 ;
;
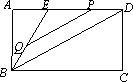
(2)当点P在线段ED的延长线上时(如图),请你猜想BE、PD、 PQ三者之间的数量关系(直接写出结果,不需说明理由);
PQ三者之间的数量关系(直接写出结果,不需说明理由);
(3)当点P运动到线段ED的中点时(如图),连结QC,过点P作PF⊥QC,垂足为F,PF交BD于点G.若BC=12,求线段PG的长.
查看答案和解析>>
科目:czsx
来源:2008年黑龙江省哈尔滨市初中毕业升学统一考试、数学试卷
题型:044
在矩形ABCD中,点E是AD边上一点,连接BE,且∠ABE=30°,BE=DE,连接BD.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.
(1)当点P在线段ED上时(如图1),求证:BE=PD+ PQ;
PQ;
(2)若BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与x的函数关系式(不要求写出自变量x的取值范围);
(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PG的长.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA,若AD=50mm,AP=80mm.
如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA,若AD=50mm,AP=80mm.
(1)判断△APB是什么三角形,证明你的结论;
(2)比较DP与PC的大小;
(3)画出以AB为直径的⊙O,交AD于点E,连接BE与AP交于点F,求tan∠AFE的值;
(4)点O′在线段AB上移动,以O’为圆心作⊙O′,使⊙O′与边AP相切,切点为M,设⊙O′的半径为m,当m为何值时,⊙O′与AP、BF都相切?
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA.
如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA.
(1)判断△APB是什么三角形,证明你的结论;
(2)比较DP与PC的大小;
(3)画出以AB为直径的⊙O,交AD于点E,连接BE与AP交于点F,若tan∠BPC= ,求tan∠AFE的值.
,求tan∠AFE的值.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
在矩形ABCD中,点E是AD边上一点,连接BE,且∠ABE=30°,BE=DE,连接BD.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.
(1)当点P在线段ED上时(如图1),求证:BE=PD+ PQ;
PQ;
(2)若BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与x的函数关系式(不要求写出自变量x的取值范围);
(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PG的长.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
在矩形ABCD中,点E是AD边上一点,连接BE,且BE=2AE,BD是∠EBC的平分线.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.
(1)当点P在线段ED上时(如图1),求证:BE=PD+ PQ;
PQ;
(2)当点P在线段ED的延长线上时(如图2),请你猜想BE,PD, PQ三者之间的数量关系(直接写出结果,不需说明理由);
PQ三者之间的数量关系(直接写出结果,不需说明理由);
(3)当点P运动到线段ED的中点时(如图3),连接QC,过点P作PF⊥QC,垂足为F,PF交BD于点G.若BC=12,求线段PG的长.

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(36):2.7 最大面积是多少(解析版)
题型:解答题
在矩形ABCD中,点E是AD边上一点,连接BE,且∠ABE=30°,BE=DE,连接BD.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.
(1)当点P在线段ED上时(如图1),求证:BE=PD+
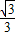
PQ;
(2)若BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与x的函数关系式(不要求写出自变量x的取值范围);
(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PG的长.

查看答案和解析>>
科目:czsx
来源:第34章《二次函数》中考题集(39):34.4 二次函数的应用(解析版)
题型:解答题
在矩形ABCD中,点E是AD边上一点,连接BE,且∠ABE=30°,BE=DE,连接BD.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.
(1)当点P在线段ED上时(如图1),求证:BE=PD+
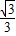
PQ;
(2)若BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与x的函数关系式(不要求写出自变量x的取值范围);
(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PG的长.
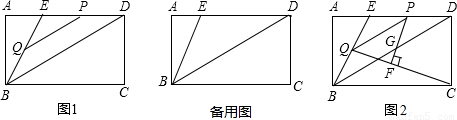
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(38):2.3 二次函数的应用(解析版)
题型:解答题
在矩形ABCD中,点E是AD边上一点,连接BE,且∠ABE=30°,BE=DE,连接BD.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.
(1)当点P在线段ED上时(如图1),求证:BE=PD+
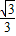
PQ;
(2)若BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与x的函数关系式(不要求写出自变量x的取值范围);
(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PG的长.

查看答案和解析>>
科目:czsx
来源:第7章《锐角三角函数》中考题集(23):7.5 解直角三角形(解析版)
题型:解答题
在矩形ABCD中,点E是AD边上一点,连接BE,且∠ABE=30°,BE=DE,连接BD.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.
(1)当点P在线段ED上时(如图1),求证:BE=PD+

PQ;
(2)若BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与x的函数关系式(不要求写出自变量x的取值范围);
(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PG的长.

查看答案和解析>>
科目:czsx
来源:第27章《二次函数》中考题集(38):27.3 实践与探索(解析版)
题型:解答题
在矩形ABCD中,点E是AD边上一点,连接BE,且∠ABE=30°,BE=DE,连接BD.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.
(1)当点P在线段ED上时(如图1),求证:BE=PD+

PQ;
(2)若BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与x的函数关系式(不要求写出自变量x的取值范围);
(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PG的长.
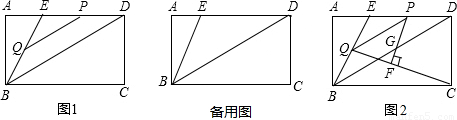
查看答案和解析>>

 用哪种方法更好呢?
用哪种方法更好呢?
 颖三位同学对此题进行探讨,给出了各自不同的证明如下:
颖三位同学对此题进行探讨,给出了各自不同的证明如下: ED∥BF.
ED∥BF.
 B.
B.
 ,你认为哪一种方法最为简捷?从中你得到什么启示?
,你认为哪一种方法最为简捷?从中你得到什么启示?











 如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA.
如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA.

 如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA,若AD=50mm,AP=80mm.
如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA,若AD=50mm,AP=80mm.![]() ;
;
![]() PQ三者之间的数量关系(直接写出结果,不需说明理由);
PQ三者之间的数量关系(直接写出结果,不需说明理由);


![]() PQ;
PQ; 如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA,若AD=50mm,AP=80mm.
如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA,若AD=50mm,AP=80mm. 如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA.
如图,在平行四边形ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA. ,求tan∠AFE的值.
,求tan∠AFE的值. PQ;
PQ;
 PQ;
PQ; PQ三者之间的数量关系(直接写出结果,不需说明理由);
PQ三者之间的数量关系(直接写出结果,不需说明理由);
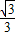 PQ;
PQ;
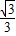 PQ;
PQ;
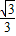 PQ;
PQ;
 PQ;
PQ;
 PQ;
PQ;