
科目:gzsx 来源:2011届福建省四地六校联考高三上学期第二次月考理科数学卷 题型:解答题
(本小题满分14分)本题(1)、(2)、(3)三个选答题,每小题7分,任选2题作答,满分14分,如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分) 选修4-2:矩阵与变换
已知 ,若
,若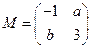 所对应的变换
所对应的变换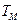 把直线
把直线 变换为自身,求实数
变换为自身,求实数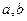 ,并求
,并求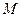 的逆矩阵。
的逆矩阵。
(2)(本题满分7分)选修4-4:坐标系与参数方程
已知直线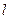 的参数方程:
的参数方程: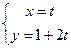 (
(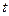 为参数)和圆
为参数)和圆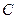 的极坐标方程:
的极坐标方程: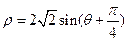 。
。
①将直线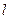 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆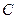 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
②判断直线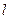 和圆
和圆 的位置关系。
的位置关系。
(3)(本题满分7分)选修4-5:不等式选讲
已知函数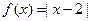
①解不等式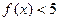 ;
;
②证明:对任意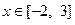 ,不等式
,不等式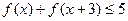 成立.
成立.
科目:gzsx 来源:2010-2011学年福建省四地六校联考高三上学期第二次月考理科数学卷 题型:解答题
(本小题满分14分)本题(1)、(2)、(3)三个选答题,每小题7分,任选2题作答,满分14分,如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分) 选修4-2:矩阵与变换
已知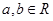 ,若
,若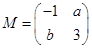 所对应的变换
所对应的变换 把直线
把直线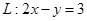 变换为自身,求实数
变换为自身,求实数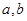 ,并求
,并求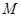 的逆矩阵。
的逆矩阵。
(2)(本题满分7分)选修4-4:坐标系与参数方程
已知直线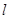 的参数方程:
的参数方程: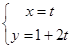 (
( 为参数)和圆
为参数)和圆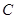 的极坐标方程:
的极坐标方程: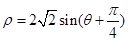 。
。
①将直线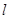 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆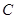 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
②判断直线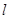 和圆
和圆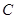 的位置关系。
的位置关系。
(3)(本题满分7分)选修4-5:不等式选讲
已知函数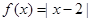
①解不等式 ;
;
②证明:对任意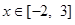 ,不等式
,不等式 成立.
成立.
科目:gzsx 来源:2006-2007年度南通市石庄中学期末数学试卷-旧人教 题型:044
设f(x)的定义在R上的奇函数,且函数y=f(x)与y=g(x)的图象关于直线x=1对称,当x>2时,g(x)=a(x-2)-(x-2)3(a为常数)
(1)求f(x)的解析式;
(2)若f(x)对区间[1,+∞)上的每个x值,恒有f(x)≥-2a成立,求a的取值范围.
科目:gzsx 来源:2011-2012学年江苏省高三第一次学情调研测试数学试卷 题型:解答题
选修4-2 矩阵与变换 已知 ,若
,若 所对应的变换
所对应的变换 把直线
把直线 变换为自身,求实数
变换为自身,求实数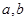 ,并求
,并求 的逆矩阵.
的逆矩阵.
科目:gzsx 来源:2013-2014学年河南郑州第四中学高二上学期第一次月考数学试卷(解析版) 题型:解答题
已知等差数列 满足:
满足: ,
, .
. 的前n项和为
的前n项和为 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)若 ,
, (
( ),求数列
),求数列 的前
的前 项和
项和 .
.
科目:gzsx 来源:2015届广东省高一下学期期末考试数学试卷(解析版) 题型:解答题
已知向量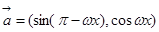 ,
,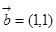 ,且
,且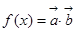 的最小正周期为
的最小正周期为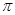
(Ⅰ)求 的值;
的值;
(Ⅱ)若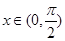 ,解方程
,解方程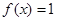 ;
;
(Ⅲ)在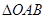 中,
中,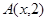 ,
,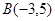 ,且
,且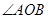 为锐角,求实数
为锐角,求实数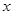 的取值范围.
的取值范围.
科目:gzsx 来源: 题型:
| 1+x |
| 1 |
| 2 |
| n |
 |
| k=2 |
| k-1 |
| k2 |
| n+1 |
| 2 |
科目:gzsx 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
| x+a |
| x+2 |
| 5 |
| 4 |
科目:gzsx 来源: 题型:
| a | x |
科目:gzsx 来源:崇明县一模 题型:解答题
| a |
| x |
科目:gzsx 来源:湖北模拟 题型:解答题
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:gzsx 来源:浦东新区二模 题型:解答题
| x+a |
| x+2 |
| 5 |
| 4 |
科目:gzsx 来源: 题型:
| 31 |
| 27 |
| 3 |
| 2 |
| 3 |