练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >指数函数求定义域

    指数函数求定义域答案解析

    科目：gzsx 来源： 题型：

    对于f(x)=log
    12
    (x2-2ax+3)    ．
    （1）函数的“定义域为R”和“值域为R”是否是一回事？分别求出实数a的取值范围；
    （2）结合“实数a的取何值时f（x）在[-1，+∞）上有意义”与“实数a的取何值时函数的定义域为（-∞，1）∪（3，+∞）”说明求“有意义”问题与求“定义域”问题的区别．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=loga(-x2+4x-3)(a＞0，且a≠1）的定义域为M．
    （Ⅰ）求定义域M，并写出f（x）的单调递增区间；
    （Ⅱ）当x∈M时，求函数g（x）=2x+3-4x的值域．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数y=x
    23
    ，（1）求定义域；（2）判断奇偶性；（3）已知该函数在第一象限的图象如图所示，试补全图象，并由图象确定单调区间．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知f（x）=loga
    1+x1-x
    （a＞0且a≠1）
    （1）求定义域  
    （2）求使f（x）＞0时，x的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=ln（1+x）+aln（1-x）（a∈R）的图象关于原点对称．
    （1）求定义域．
    （2）求a的值．
    （3）若g(x)=ef(x)-
    1-m2+m
    有零点，求m的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    直线l：x-ky+2
    		2
    =0    与圆O：x2+y2=4相交于A，B两点，O为原点，△ABO的面积为S．
    （1）试将S表示为k的函数S（k），并求定义域；
    （2）求S的最大值，并求此时直线l的方程．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    对于定义域为[0，1]的函数f（x）如果满足以下三个条件：①对任意的x∈[0，1]，总有f（x）≥2；②f（1）=3；③若x1≥0，x2≥0，x1+x2≤1，都有f（x1+x2）≥f（x1）+f（x2）-2成立．则称函数f（x）为理想函数．
    （1）判断函数g（x）=2x+1 （0≤x≤1）是否为理想函数，并予以证明；
    （2）求定义域为[0，1]的理想函数f（x）的最大值和最小值；
    （3）某同学发现：当x=
    1
    2n
    （n∈N）时，有f（
    1
    2n
    ）≤
    1
    2n
    +2，由此他提出猜想：对一切x∈（0，1]，都有f（x）＜2x+2，请你根据该同学发现的结论（或其它方法）来判断此猜想是否正确，并说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    关于指数函数，有下列几个命题：
    ①指数函数的定义域为（0，+∞）；
    ②指数函数的值域是不包括1的；
    ③指数函数f（x）=2x和f（x）=（
    12
    ）x关于y轴对称；
    ④指数函数都是单调函数．
    其中正确的命题有
    ③④
    ③④
     （填写正确命题的序号）．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    A、B两城相距100km，在两地之间距A城xkm处D地建一核电站给A、B两城供电，为保证城市安全．核电站距市距离不得少于10km．已知供电费用与供电距离的平方和供电量之积成正比，比例系数λ=0.25．若A城供电量为20亿度/月，B城为10亿度/月．
    （Ⅰ）把月供电总费用y表示成x的函数，并求定义域；
    （Ⅱ）核电站建在距A城多远，才能使供电费用最小．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    求定义域：y=
    1
    2-|x|
    +
    		x2-1
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    10、已知y=log4（2x+3-x2）．
    （1）求定义域；
    （2）求f（x）的单调区间；
    （3）求y的最大值，并求取得最大值的x值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=ax2+ln（x+1），（a∈R）．
    （Ⅰ）设函数Y=F（X-1）定义域为D
    ①求定义域D；
    ②若函数h（x）=x4+[f（x）-ln（x+1）]（x+
    1
    x
    ）+cx2+f′（0）在D上有零点，求a2+c2的最小值；
    （Ⅱ） 当a=
    1
    2
    时，g（x）=f′（x-1）+bf（x-1）-ab（x-1）2+2a，若对任意的x∈[1，e]，都有
    2
    e
    ≤g（x）≤2e恒成立，求实数b的取值范围；（注：e为自然对数的底数）
    （Ⅲ）当x∈[0，+∞）时，函数y=f（x）图象上的点都在
    x≥0
    y-x≤0
    所表示的平面区域内，求实数a的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    若函数f(x)=log
    		2
    (1-x2)    ，
    （1）求定义域；
    （2）求值域；
    （3）求单调增区间．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    1、求定义域时，应注意以下几种情况．
    （1）如果f（x）是整式，那么函数的定义域是
    R
    ；
    （2）如果f（x）是分式，那么函数的定义域是使
    分母不等于零
    的实数的集合；
    （3）如果f（x）为二次根式，那么函数的定义域是使
    被开方数不小于零
    的实数的集合；
    （4）如果f（x）为某一数的零次幂，那么函数的定义域是使
    底数不为零
    的实数的集合．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    如图：A、B两城相距100km，某天燃气公司计划在两地之间建一天燃气站D 给A、B两城供气．已知D地距A城x km，为保证城市安全，天燃气站距两城市的距离均不得少于10km．已知建设费用y （万元）与A、B两地的供气距离（km）的平方和成正比，当天燃气站D距A城的距离为40km时，建设费用为1300万元．（供气距离指天燃气站距到城市的距离）
    （1）把建设费用y（万元）表示成供气距离x （km）的函数，并求定义域；
    （2）天燃气供气站建在距A城多远，才能使建设供气费用最小．最小费用是多少？

    查看答案和解析>>

    科目：gzsx 来源： 题型：

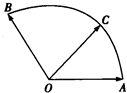    精英家教网 如图，给定两个长度为1的平面向量
    OA
    和
    OB
    ，它们的夹角为
    2π
    3
    ，点C是以O为圆心的圆弧
    AB
    上的一个动点，且
    OC
    =x
    OA
    +y
    OB
    （x，y∈
    .
    R-
    ）
    （Ⅰ）设∠AOC=θ，写出x，y关于θ的函数解析式并求定义域；
    （Ⅱ）求x+y的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    A，B两城相距100km，在两地之间距A城xkm处D地建一核电站给A，B两城供电．为保证城市安全，核电站距城市距离不得少于45km．已知供电费用（元）与供电距离（km）的平方和供电量（亿度）之积成正比，比例系数λ=0.2，若A城供电量为30亿度/月，B城为20亿度/月．
    （Ⅰ）把月供电总费用y表示成x的函数，并求定义域；
    （Ⅱ）核电站建在距A城多远，才能使供电费用最小，最小费用是多少？

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知A、B两城相距100km，在两地之间距A城xkm处D地建一核电站给A、B两城供电，为保证城市安全．核电站距市距离不得少于10km．已知供电费用与供电距离的平方和供电量之积成正比，比例系数λ=0.3．若A城供电量为20亿度/月，B城为10亿度/月．
    （1）把月供电总费用y表示成x的函数，并求定义域；
    （2）核电站建在距A城多远，才能使供电费用最小．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    有一海湾，海岸线为近似半个椭圆（如图），椭圆长轴端点为A，B，AB间距离为3km，椭圆焦点为C，D，CD间距离为2km，在C，D处分别有甲，乙两个油井，现准备在海岸线上建一度假村P，不考虑风向等因素影响，油井对度假村废气污染程度与排出废气的浓度成正比（比例系数都为k1），与距离的平方成反比（比例系数都为k2），又知甲油井排出的废气浓度是乙的8倍．
    （1）设乙油井排出的浓度为a（a为常数）度假村P距离甲油井xkm，度假村P受到甲乙两油井的污染程度和记为f（x），求f（x）的表达式并求定义域；
    （2）度假村P距离甲油井多少时，甲乙两油井对度假村的废气污染程度和最小？

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （1）化简：
    tan(2π-α)sin(-2π-α)cos(6π-α)
    sin(α+
    3π
    2
    )cos(α+
    3π
    2
    )tan(-α)
    ；
    （2）求定义域：y=lg（3-4sin2x）

    查看答案和解析>>