
科目:gzsx 来源: 题型:
| 喜欢数学课程 | 不喜欢数学课程 | 总计 |
男 | 37 | 85 | 122 |
女 | 35 | 143 | 178 |
总计 | 72 | 228 | 300 |
由表中的数据,你认为在多大程度上可以认为高中生的性别与是否喜欢数学课程之间有关系?为什么?
科目:gzsx 来源: 题型:
| 喜欢数学课程 | 不喜欢数学课程 | 总计 |
男 | 37 | 85 | 122 |
女 | 35 | 143 | 178 |
总计 | 72 | 228 | 300 |
你认为性别与是否喜欢数学课程之间有关系的把握有( )
A.0 B.95% C.99% D.100%
科目:gzsx 来源:导学大课堂选修数学2-3苏教版 苏教版 题型:013
为了考察高中生的性别与是否喜欢数学课程之间的关系,在某校高中生中随机抽取了300名学生,得到如下列联表:

你认为性别与是否喜欢数学课程之间有关系的把握有
0
95%
99%
100%
科目:gzsx 来源:江西省新余一中2012届高三第三模拟考试数学文科试题 题型:013
为考察高中生的性别与是否喜欢数学课程之间的关系,在江西省某示范性高中的学生中随机抽取50名学生,得到如下联表,那么下列判断正确的是
参考公式和数值;
![]() ,
,![]() ≈4.844
≈4.844
A.约有90%的把握认为“性别与喜欢数学课程之间有关系”
B.约有99%的把握认为“性别与喜欢数学课程之间有关系”
C.在犯错概率不超过0.05前提下认为“性别与喜欢数学课之间有关系”;
D.在犯错概率不超过0.01前提下认为“性别与喜欢数学课之间有关系”;
科目:gzsx 来源: 题型:
性别与喜欢数学课列联表
| 喜欢数学课 | 不喜欢数学课 | 合计 |
男 | 37 | 85 | 122 |
女 | 35 | 143 | 178 |
合计 | 72 | 228 | 300 |
由表中的数据计算得K2≈4.513.高中生的性别与是否喜欢数学课之间是否有关系?为什么?
科目:gzsx 来源:导学大课堂选修数学2-3苏教版 苏教版 题型:044
为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中随机抽取300名学生,得到如下列联表:

由表中数据计算得χ2≈4.513.高中生的性别与是否喜欢数学课程之间是否有关系?为什么?
科目:gzsx 来源: 题型:
为了考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校的高中生中随机地抽取了300名学生进行调查,得到如下列联表:
| 喜欢数学 | 不喜欢数学 | 总计 | |
| 男 | 37 | 85 | 122 |
| 女 | 35 | 143 | 178 |
| 总计 | 72 | 228 | 300 |
由表中数据计算![]() ,判断高中生的性别与是否喜欢数学课程之间是否有关系,并说明理由.
,判断高中生的性别与是否喜欢数学课程之间是否有关系,并说明理由.
科目:gzsx 来源: 题型:
性别与喜欢理科课程列联表
| 喜欢理科课程 | 不喜欢理科课程 | 总 计 |
男 | 37 | 85 | 122 |
女 | 35 | 143 | 178 |
总 计 | 72 | 228 | 300 |
由表中数据计算K2≈4.513.高中生的性别与是否喜欢理科课程之间是否有关系?为什么?
科目:gzsx 来源: 题型:
| 评价等级(分) | 0-1.0 | 1.1-2.0 | 2.1-3.0 | 3.1-4.0 | 4.1-5.0 |
| 女(人数) | 2 | 7 | 9 | 20 | 12 |
| 男(人数) | 3 | 9 | 18 | 12 | 8 |
| 喜欢该商品 | 不喜欢该商品 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:gzsx 来源: 题型:解答题
| 评价等级(分) | 0-1.0 | 1.1-2.0 | 2.1-3.0 | 3.1-4.0 | 4.1-5.0 |
| 女(人数) | 2 | 7 | 9 | 20 | 12 |
| 男(人数) | 3 | 9 | 18 | 12 | 8 |
| 喜欢该商品 | 不喜欢该商品 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 |
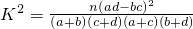 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:gzsx 来源:2012-2013学年广东省珠海四中高三(上)摸底数学试卷(文科)(解析版) 题型:解答题
| 评价等级(分) | 0-1.0 | 1.1-2.0 | 2.1-3.0 | 3.1-4.0 | 4.1-5.0 |
| 女(人数) | 2 | 7 | 9 | 20 | 12 |
| 男(人数) | 3 | 9 | 18 | 12 | 8 |
| 喜欢该商品 | 不喜欢该商品 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 |
 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:gzsx 来源:101网校同步练习 高二数学 人教社(新课标B 2004年初审通过) 人教实验版 题型:044
为考察高中生的性别与是否喜欢数学之间的关系,在某城市的某校高中生中随机抽取300名学生,得到如下列联表:

根据表中的数据判断,高中生的性别与是否喜欢数学是否有关系?
科目:gzsx 来源: 题型:
| 男 | 女 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
| p(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005] | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
科目:gzsx 来源:2014届广东省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
性别与看营养说明列联表 单位: 名
|
|
男 |
女 |
总计 |
|
看营养说明 |
50 |
30 |
80 |
|
不看营养说明 |
10 |
20 |
30 |
|
总计 |
60 |
50 |
110 |
(1)从这50名女生中按是否看营养说明采取分层抽样,抽取一个容量为10的样本,问样本中看与不看营养说明的女生各有多少名?
(2)根据以上列联表,能否在犯错误的概率不超过0.01的前提下认为性别与是否看营养说明之间有关系?
下面的临界值表供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
科目:gzsx 来源: 题型:
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥K0) | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:gzsx 来源:2012届山东省高二下学期期末考试数学(理) 题型:选择题
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了下表:
|
|
喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
男生 |
20 |
5 |
25 |
|
女生 |
10 |
15 |
25 |
|
合计 |
30 |
20 |
50 |
则根据表中的数据,计算随机变量 的值,并参考有关公式,你认为性别与是否喜爱打篮球之间有关系的把握有
的值,并参考有关公式,你认为性别与是否喜爱打篮球之间有关系的把握有
A.0
B. C .99.5% D.
C .99.5% D.
科目:gzsx 来源: 题型:解答题
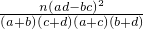 ,其中n=a+b+c+d为样本容量
,其中n=a+b+c+d为样本容量| P(K2≥K0) | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:gzsx 来源:2009-2010学年河南省漯河市临颍二高高二(下)期中数学试卷(文科)(解析版) 题型:解答题
 ,其中n=a+b+c+d为样本容量
,其中n=a+b+c+d为样本容量| P(K2≥K) | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 5.024 | 6.635 | 7.879 | 10.828 |
科目:gzsx 来源:不详 题型:解答题
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥K0) | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:gzsx 来源: 题型:
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了下表:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
则根据表中的数据,计算随机变量![]() 的值,并参考有关公式,你认为性别与是否喜爱打篮球之间有关系的把握有
的值,并参考有关公式,你认为性别与是否喜爱打篮球之间有关系的把握有
A.0 B.![]() C .99.5% D.
C .99.5% D.![]()