练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >（2013?常州）在Rt△ABC中，∠C

    （2013?常州）在Rt△ABC中，∠C答案解析

    科目：czsx 来源： 题型：

    （2013•常州）在Rt△ABC中，∠C=90°，AC=1，BC=
    		3
    ，点O为Rt△ABC内一点，连接A0、BO、CO，且∠AOC=∠COB=BOA=120°，按下列要求画图（保留画图痕迹）：
    以点B为旋转中心，将△AOB绕点B顺时针方向旋转60°，得到△A′O′B（得到A、O的对应点分别为点A′、O′），并回答下列问题：
    ∠ABC=
    30°
    30°
    ，∠A′BC=
    90°
    90°
    ，OA+OB+OC=
    		7
    		7
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•牡丹江）在Rt△ABC中，CA=CB，AB=9
    		2
    ，点D在BC边上，连接AD，若tan∠CAD=
    1
    3
    ，则BD的长为
    6
    6
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•杭州）在Rt△ABC中，∠C=90°，若AB=4，sinA=
    3
    5
    ，则斜边上的高等于（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•杭州）在Rt△ABC中，∠C=90°，AB=2BC，现给出下列结论：①sinA=
    		3
    2
    ；②cosB=
    1
    2
    ；③tanA=
    		3
    3
    ；④tanB=
    		3
    ，其中正确的结论是
    ②③④
    ②③④
    （只需填上正确结论的序号）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•德宏州）在Rt△ABC中，∠C=90°，AB=10．若以点C为圆心，CB为半径的圆恰好经过AB的中点D，则AC=（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

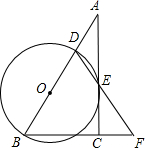    （2013•宁夏）在Rt△ABC中，∠ACB=90°，D是AB边上的一点，以BD为直径作⊙O交AC于点E，连结DE并延长，与BC的延长线交于点F．且BD=BF．
    （1）求证：AC与⊙O相切．
    （2）若BC=6，AB=12，求⊙O的面积．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•汕头）在Rt△ABC中，∠ABC=90°，AB=3，BC=4，则sinA=
    4
    5
    4
    5
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•抚顺）在Rt△ABC中，∠ACB=90°，∠A=30°，点D是AB的中点，DE⊥BC，垂足为点E，连接CD．
    （1）如图1，DE与BC的数量关系是
    DE=
    		3
    2
    BC
    DE=
    		3
    2
    BC
    ；
    （2）如图2，若P是线段CB上一动点（点P不与点B、C重合），连接DP，将线段DP绕点D逆时针旋转60°，得到线段DF，连接BF，请猜想DE、BF、BP三者之间的数量关系，并证明你的结论；
    （3）若点P是线段CB延长线上一动点，按照（2）中的作法，请在图3中补全图形，并直接写出DE、BF、BP三者之间的数量关系．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•连云港）在Rt△ABC中，∠C=90°，若sinA=
    5
    13
    ，则cosA的值为（　　）

    查看答案和解析>>

    科目：czsx 来源：2010年全国中考数学试题汇编《锐角三角函数》（03）（解析版） 题型：填空题

    （2010•常州）在Rt△ABC中，∠C=90°，AC=2，BC=1，则tanB=    ，sinA=    ．

    查看答案和解析>>

    科目：czsx 来源：2010年江苏省常州市中考数学试卷（解析版） 题型：填空题

    （2010•常州）在Rt△ABC中，∠C=90°，AC=2，BC=1，则tanB=    ，sinA=    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

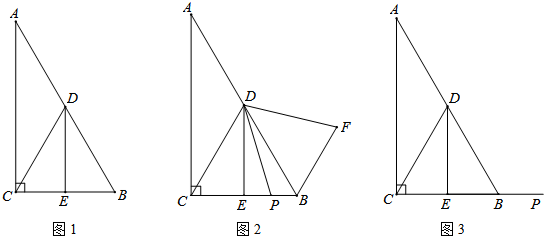
    （2013•常州模拟）如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=1，点D在AC上，将△ADB沿直线BD翻折后，将点A落在点E处，如果AD⊥ED，那么线段DE的长为（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

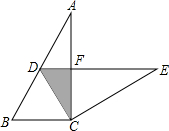    （2013•呼伦贝尔）如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=2，将△ABC绕点C顺时针方向旋转60°后得到△EDC，此时点D在斜边AB上，斜边DE交AC于点F．则图中阴影部分的面积为（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•邵阳）如图所示，在Rt△ABC中，AB=BC=4，∠ABC=90°，点P是△ABC的外角∠BCN的角平分线上一个动点，点P′是点P关于直线BC的对称点，连结PP′交BC于点M，BP′交AC于D，连结BP、AP′、CP′．
    （1）若四边形BPCP′为菱形，求BM的长；
    （2）若△BMP′∽△ABC，求BM的长；
    （3）若△ABD为等腰三角形，求△ABD的面积．

    查看答案和解析>>

    科目：czsx 来源： 题型：

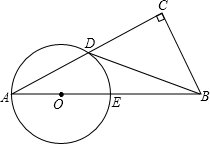    （2013•大港区一模）如图，在Rt△ABC中，∠C=90°，∠A+∠CDB=90°，过点A、D作⊙O，使圆心O在AB上，⊙O与AB交于点E．
    （Ⅰ）求证：直线BD与⊙A相切；
    （Ⅱ）若点D是AC的中点，BC=12，求AD的长．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•集美区一模）在Rt△ABC中，∠C=90°，当∠B=
    50
    50
    度时，命题“如果tanB≥1，那么
    		2
    2
    ≤sinA≤
    		3
    2
    ．”不成立．

    查看答案和解析>>

    科目：czsx 来源： 题型：

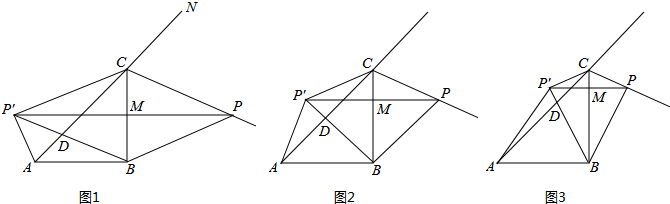
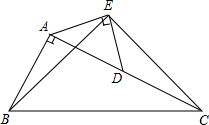    （2013•大兴区二模）已知：如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，以AD为斜边在△ABC外作等腰直角三角形AED，连结BE、EC．试猜想线段BE和EC的数量关系及位置关系，并证明你的猜想．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•香坊区一模）如图，在Rt△ABC中，CD是斜边AB上的高，点F在CD上，DH⊥BF且与AC的延长线交于点E．若AC=
    		6
    CF，CD=3，则AE的长为
    3
    		6
    3
    		6
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•德庆县一模）如图，在Rt△ABC中，∠C=90°．
    （1）用直尺和圆规作△ABC的BC边上的垂直平分线，与AB交于D点，与BC交于E点（保留作图痕迹，不写作法）；
    （2）若AC=6，AB=10，连结CD，求DE，CD的长．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•河西区一模）如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，点E在AC上（点E与A、C都不重合），点F在斜边AB上（点F与A、B都不重合）．
    （Ⅰ）若EF平分Rt△ABC的周长，设AE=x，△AEF的面积为y，写出y与x之间的函数关系式，并指出x的取值范围；
    （Ⅱ）试问：是否存在直线EF将Rt△ABC的周长和面积同时平分？若存在，求出AE的长；若不存在，说明理由．

    查看答案和解析>>