
科目:czsx 来源: 题型:
如图,在直角坐标系中,已知点A(-3,0),B(0,4), 对 ![]() 连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________
连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________

科目:czsx 来源: 题型:
如图,在直角坐标系中,已知点A(-3,0),B(0,4), 对 ![]() 连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________
连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________

科目:czsx 来源: 题型:
如图,在直角坐标系中,已知点A(-3,0),B(0,4),对![]() 连续作旋转变换,依次得带三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为__________
连续作旋转变换,依次得带三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为__________

| |
科目:czsx 来源:2012年初中毕业升学考试(江苏盐城卷)数学(解析版) 题型:解答题
在平面直角坐标系 中,已知二次函数
中,已知二次函数 的图象经过点
的图象经过点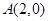 和点
和点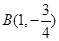 ,直线
,直线 经过抛物线的顶点且与
经过抛物线的顶点且与 轴垂直,垂足为
轴垂直,垂足为 .
.
1.求该二次函数的表达式;
2.设抛物线上有一动点 从点
从点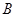 处出发沿抛物线向上运动,其纵坐标
处出发沿抛物线向上运动,其纵坐标 随时间
随时间
 ≥
≥ )的变化规律为
)的变化规律为 .现以线段
.现以线段 为直径作
为直径作 .
.
①当点 在起始位置点
在起始位置点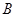 处时,试判断直线
处时,试判断直线 与
与 的位置关系,并说明理由;在点
的位置关系,并说明理由;在点 运动的过程中,直线
运动的过程中,直线 与
与 是否始终保持这种位置关系? 请说明你的理由;
是否始终保持这种位置关系? 请说明你的理由;
②若在点 开始运动的同时,直线
开始运动的同时,直线 也向上平行移动,且垂足
也向上平行移动,且垂足 的纵坐标
的纵坐标 随时间
随时间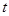 的变化规律为
的变化规律为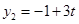 ,则当
,则当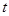 在什么范围内变化时,直线
在什么范围内变化时,直线 与
与 相交? 此时,若直线
相交? 此时,若直线 被
被 所截得的弦长为
所截得的弦长为 ,试求
,试求 的最大值.
的最大值.

科目:czsx 来源:2012年北师大版初中数学九年级下3.7弧长及扇形的面积练习卷(解析版) 题型:选择题
如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴、y轴分别交于A、B两点,B点坐标为(0,2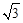 ),OC与⊙D相交于点C,∠OCA=30°,则图中阴影部分的面积为(
)
),OC与⊙D相交于点C,∠OCA=30°,则图中阴影部分的面积为(
)

A. B.
B. C.
C. ; D.
; D.
科目:czsx 来源:2012年初中毕业升学考试(江苏盐城卷)数学(带解析) 题型:解答题
在平面直角坐标系 中,已知二次函数
中,已知二次函数 的图象经过点
的图象经过点 和点
和点 ,直线
,直线 经过抛物线的顶点且与
经过抛物线的顶点且与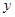 轴垂直,垂足为
轴垂直,垂足为 .
.
【小题1】求该二次函数的表达式;
【小题2】设抛物线上有一动点 从点
从点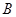 处出发沿抛物线向上运动,其纵坐标
处出发沿抛物线向上运动,其纵坐标 随时间
随时间 ≥
≥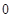 )的变化规律为
)的变化规律为 .现以线段
.现以线段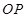 为直径作
为直径作 .
.
①当点 在起始位置点
在起始位置点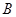 处时,试判断直线
处时,试判断直线 与
与 的位置关系,并说明理由;在点
的位置关系,并说明理由;在点 运动的过程中,直线
运动的过程中,直线 与
与 是否始终保持这种位置关系? 请说明你的理由;
是否始终保持这种位置关系? 请说明你的理由;
②若在点 开始运动的同时,直线
开始运动的同时,直线 也向上平行移动,且垂足
也向上平行移动,且垂足 的纵坐标
的纵坐标 随时间
随时间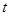 的变化规律为
的变化规律为 ,则当
,则当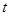 在什么范围内变化时,直线
在什么范围内变化时,直线 与
与 相交? 此时,若直线
相交? 此时,若直线 被
被 所截得的弦长为
所截得的弦长为 ,试求
,试求 的最大值.
的最大值.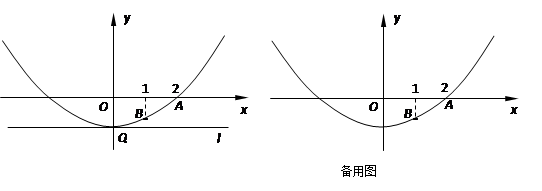
科目:czsx 来源:2013-2014学年山东烟台海阳市九年级上期末数学试卷(解析版) 题型:解答题
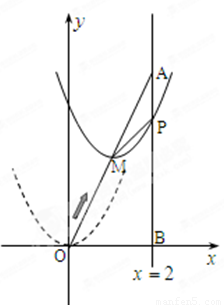
如图,在平面直角坐标系中,已知点 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与 轴相交于点
轴相交于点 ,连结
,连结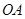 ,抛物线y=x
,抛物线y=x
 从点
从点 沿
沿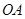 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点 ,顶点
,顶点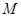 到
到 点时停止移动.
点时停止移动.
(1)求线段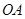 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点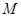 的横坐标为
的横坐标为 ,
,
①用 的代数式表示点
的代数式表示点 的坐标;
的坐标;
②当 为何值时,线段
为何值时,线段 最短;
最短;
(3)当线段 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点 ,使△
,使△ 的面积与△
的面积与△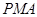 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
科目:czsx 来源:2013-2014学年福建省厦门市九年级上学期质量检测数学试卷(解析版) 题型:解答题
(1)计算 ;
;
(2)在平面直角坐标系中,已知点A(2,1),B(2,0),C(1,-1),请在图上画出△ABC,并画出与△ABC关于原点O对称的图形;

(3)如图,AB是⊙O的直径,直线AC,BD是⊙O的切线,A,B是切点.求证:AC∥BD.

科目:czsx 来源:江苏中考真题 题型:解答题
 中,已知二次函数
中,已知二次函数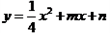 的图象经过点
的图象经过点 和点
和点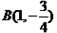 ,直线
,直线 经过抛物线的顶点且与
经过抛物线的顶点且与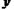 轴垂直,垂足为
轴垂直,垂足为 .
.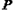 从点
从点 处出发沿抛物线向上运动,其纵坐标
处出发沿抛物线向上运动,其纵坐标 随时间
随时间 ≥
≥ )的变化规律为
)的变化规律为 .现以线段
.现以线段 为直径作⊙C.
为直径作⊙C. 在起始位置点
在起始位置点 处时,试判断直线
处时,试判断直线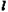 与⊙C的位置关系,并说明理由;在点
与⊙C的位置关系,并说明理由;在点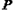 运动的过程中,直线
运动的过程中,直线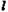 与⊙C是否始终保持这种位置关系? 请说明你的理由;
与⊙C是否始终保持这种位置关系? 请说明你的理由; 开始运动的同时,直线
开始运动的同时,直线 也向上平行移动,且垂足
也向上平行移动,且垂足 的纵坐标
的纵坐标 随时间
随时间 的变化规律为
的变化规律为 ,则当
,则当 在什么范围内变化时,直线
在什么范围内变化时,直线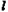 与⊙C相交? 此时,若直线
与⊙C相交? 此时,若直线 被⊙C所截得的弦长为
被⊙C所截得的弦长为 ,试求
,试求 的最大值.
的最大值.
科目:czsx 来源: 题型:044
在平面直角坐标系中,已知A(0,2),B(4,0),设P、Q分别是线段AB、OB上的动点,它们同时出发,点P以每秒3个单位的速度从点A向点B运动,点Q以每秒1个单位的速度从点B向点O运动.设运动时间为t(秒).

(1)
用含t的代数式表示点P的坐标;(2)
当t为何值时,△OPQ为直角三角形(3)
在什么条件下,以Rt△OPQ的三个顶点能确定一条对称轴平行于y轴的抛物线?选择一种情况,求出所确定的抛物线的解析式.科目:czsx 来源: 题型:
在平面直角坐标系中,已知四边形OABC是平行四边形,![]() ,
,
OC=4,OA=8,动点P从点O开始,以每秒1个单位的速度沿O→A→B运动,点Q同时从点O开始,
以每秒1个单位的速度沿O→C→B运动,其中一点到达B时,另一点也随之停![]() 止运动,设运动时间
止运动,设运动时间
为t秒.
(1) 填空:点B的坐标为B( , ),对角线OB的长度为__________;
(2) 设△OPQ的面积为S,求S与t的函数关系式.
 | |||||
 |  | ||||
科目:czsx 来源: 题型:
在平面直角坐标系![]() 中,已知二次函数
中,已知二次函数![]() 的图象经过点
的图象经过点![]() 和点
和点![]() ,直线
,直线![]() 经过抛物线的顶点且与
经过抛物线的顶点且与![]() 轴垂直,垂足为
轴垂直,垂足为![]() .
.
(1) 求该二次函数的表达式;
(2) 设抛物线上有一动点![]() 从点
从点![]() 处出发沿抛物线向上运动,其纵坐标
处出发沿抛物线向上运动,其纵坐标![]() 随时间
随时间
![]() ≥
≥![]() )的变化规律为
)的变化规律为![]() .现以线段
.现以线段![]() 为直径作
为直径作![]() .
.
①当点![]() 在起始位置点
在起始位置点![]() 处时,试判断直线
处时,试判断直线![]() 与
与![]() 的位置关系,并说明理由;在点
的位置关系,并说明理由;在点![]() 运动的过程中,直线
运动的过程中,直线![]() 与
与![]() 是否始终保持这种位置关系? 请说明你的理由;
是否始终保持这种位置关系? 请说明你的理由;
②若在点![]() 开始运动的同时,直线
开始运动的同时,直线![]() 也向上平行移动,且垂足
也向上平行移动,且垂足![]() 的纵坐标
的纵坐标![]() 随时间
随时间![]() 的变化规律为
的变化规律为![]() ,则当
,则当![]() 在什么范围内变化时,直线
在什么范围内变化时,直线![]() 与
与![]() 相交? 此时,若直线
相交? 此时,若直线![]() 被
被![]() 所截得的弦长为
所截得的弦长为![]() ,试求
,试求![]() 的最大值.
的最大值.
 |
科目:czsx 来源: 题型:
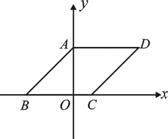
如图,将边长为![]() 的菱形ABCD纸片放置在平面直角坐标系中.已知∠B=45°.
的菱形ABCD纸片放置在平面直角坐标系中.已知∠B=45°.
(1)画出边AB沿y轴对折后的对应线段![]() ,
,![]() 与边CD交于点E;
与边CD交于点E;
(2)求![]() 出线段
出线段 ![]() 的长;
的长;
(3)求点E的坐标.
 |
科目:czsx 来源: 题型:013
则BD∶DC等于
[ ]
A.1∶![]() B.1∶2 C.1∶4 D.2∶1
B.1∶2 C.1∶4 D.2∶1
科目:czsx 来源: 题型:
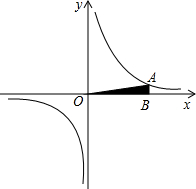 (2012•和平区二模)如图,在直角坐标系中,O为坐标原点.已知反比例函数y=
(2012•和平区二模)如图,在直角坐标系中,O为坐标原点.已知反比例函数y=| k |
| x |
| 1 |
| 2 |
| k |
| x |
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
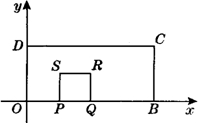 28、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.
28、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.