科目:czsx 来源: 题型:
 (2013•甘井子区一模)如图,直线y=k1x+b与双曲线y=
(2013•甘井子区一模)如图,直线y=k1x+b与双曲线y=| k2 |
| x |
| k2 |
| x |
科目:czsx 来源: 题型:
 如图,直线y=k1x+b与双曲线y=
如图,直线y=k1x+b与双曲线y=| a |
| x |
| a |
| x |
科目:czsx 来源: 题型:
 (2013•阜宁县一模)如图,直线y=k1x-b与双曲线y=
(2013•阜宁县一模)如图,直线y=k1x-b与双曲线y=| k2 |
| x |
| k2 |
| x |
科目:czsx 来源: 题型:
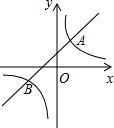 (2012•襄阳)如图,直线y=k1x+b与双曲线y=
(2012•襄阳)如图,直线y=k1x+b与双曲线y=| k2 |
| x |
| k2 |
| x |
科目:czsx 来源: 题型:
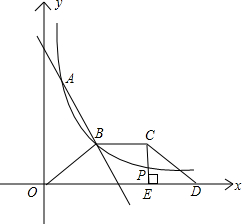
| k2 |
| x |
| k2 |
| x |
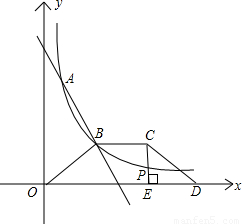
科目:czsx 来源: 题型:
| k2 |
| x |
 两点.
两点.| k2 |
| x |
科目:czsx 来源: 题型:
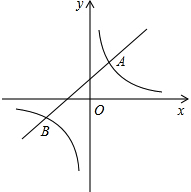 (2013•昭通)如图,直线y=k1x+b(k1≠0)与双曲线y=
(2013•昭通)如图,直线y=k1x+b(k1≠0)与双曲线y=| k2 | x |
科目:czsx 来源: 题型:
 (2013•攀枝花)如图,直线y=k1x+b(k1≠0)与双曲线y=
(2013•攀枝花)如图,直线y=k1x+b(k1≠0)与双曲线y=| k2 |
| x |
| k2 |
| x |
科目:czsx 来源: 题型:
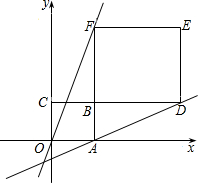 (2013•南通一模)如图,直线y1=k1x-1与x轴正半轴交于点A(2,0),以OA为边在x轴上方作正方形OABC,延长CB交直线y1于点D,再以BD为边向上作正方形BDEF.
(2013•南通一模)如图,直线y1=k1x-1与x轴正半轴交于点A(2,0),以OA为边在x轴上方作正方形OABC,延长CB交直线y1于点D,再以BD为边向上作正方形BDEF.科目:czsx 来源: 题型:
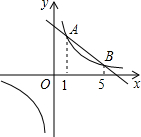 (2012•连云港)如图,直线y=k1x+b与双曲线y=
(2012•连云港)如图,直线y=k1x+b与双曲线y=| k2 |
| x |
| k2 |
| x |
科目:czsx 来源: 题型:
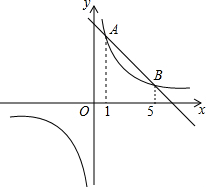 如图,直线y1=k1x+b与双曲线y2=
如图,直线y1=k1x+b与双曲线y2=| k2 |
| x |
| k2 |
| x |
科目:czsx 来源:2010年10月浙江省杭州市滨江区九年级(上)月考数学试卷(解析版) 题型:解答题
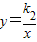 (x>0)的图象交于A(1,6),B(a,3)两点.
(x>0)的图象交于A(1,6),B(a,3)两点. 时x的取值范围;
时x的取值范围;