练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >在（-2）三次方，-（-2）三次方

    在（-2）三次方，-（-2）三次方答案解析

    科目：czsx 来源： 题型：

    在△ABC中，三个内角的度数均为整数，且∠A＜∠B＜∠C，4∠C=7∠A，则∠B的度数为
     
    度．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    在同一平面内有不在同一直线的三个点，以这三个点为顶点的平行四边形有（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图所示，在数轴上有三个点，A，B，C，它们所表示的数分别为-3、-2、2，试回答下列问题．
    （1）A，C两点间的距离是
    5
    5
    ；
    （2）若E点与B点的距离是8，则E点表示的数是
    6或-10
    6或-10
    ；
    （3）若将数轴折叠，使A点与C点重合，则点B与数
    1
    1
    表示的点重合．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知可以在右侧5×5的表中的21个空格填入整数，使得：
    （1）在每横行的三个相邻的数，最左、最右的两个数的平均值等于中间的数；
    （2）在每竖列的三个相邻的数，最上、最下的两个数的平均值等于中间的数．则表格中记有﹡号的空格的数是
     
    ．
    ﹡
    74
    186
    103
    0

    查看答案和解析>>

    科目：czsx 来源： 题型：

    31、在等腰三角形的三个外角中，最多有（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

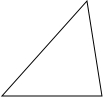    作图题：
    （1）如图，一个三角形状的水池，现要在水池内安装一个喷水头，且喷水头到池边的距离都要相等，请用尺规找出喷水池的位置点P．
    （2）先用圆规画一个圆，然后在圆弧上确定三个点A、B、C，作线段AB、BC的垂直平分线，你能发现什么结论？

    查看答案和解析>>

    科目：czsx 来源： 题型：

    把自然数1，2，3，4，…2n随意放置在一个圆周上，据统计，在所有相邻的三个数中，三个数全为奇数的有a组，三个数中恰有两个为奇数的有b组，三个数中恰有一个为奇数的有c组，三个数都为偶数的有d组，如果a-d≠0，那么
    b-ca-d
    的值为
     
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    三张卡片的正反面上分别写有数字0与2，3与4，5与6，把这三张卡片拼在一起表示一个三位数，则这个三位数是偶数的概率是
     
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    若正方形的四个顶点分别在直角三角形的三条边上，直角三角形的两直角边的长分别为3cm和4cm，则此正方形的边长为
     
    cm．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    9、平面直角坐标系内，一个圆心在（a，b）的圆包含原点（0，0），设此圆在第一象限及第三象限的面积和为S1，在第二象限及第四象限的面积和为S2，则|S1-S2|=
    4|ab|
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

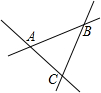    精英家教网在公园里有三条互相交织的小路，如图，现在公园的管理人员向在这三条小路所围成的三角形区域内建一小亭供人们休息，且小亭中心到三条小路的距离相等，假如你是公园的管理人员，请试确定小亭的中心位置（　　）
    A、在△ABC三条中线的交点B、在△ABC三条角平分线的交点C、在△ABC三条高线的交点D、在△ABC三边垂直平分线的交点

    查看答案和解析>>

    科目：czsx 来源： 题型：

    17、在△ABC中，三个内角的度数比为2：3：4；则相应的外角度数的比是
    7：6：5
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图，Rt△ABC中，∠A=90°，四边形AEDF为正方形，E、D、F分别在Rt△ABC的三边上，BD=7.5，CD=4，图中阴影部分的面积之和为
    15
    15
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    100年前，豪华游轮“泰坦尼克号”发生海难沉入大西洋．这是和平时期死伤人数最惨重的海难之一，也是最广为人知的海上事故之一．
    成员 成员级别 乘员总人数 获救比率 死亡比率 获救人数 死亡人数
    儿童 头等舱 6 85% 17% 5 1
    二等舱 24 100% 0% 24 0
    三等舱 79 34% 66% 27 52
    女子 头等舱 144 97% 3% 140 4
    二等舱 93 86% 14% 80 13
    三等舱 165 46% 54% 76 89
    船员 23 87% 13% 20 3
    男子 头等舱 175 33% 67% 57 118
    二等舱 168 8% 92% 14 154
    三等舱 462 16% 84% 75 387
    船员 885 22% 78% 192 693
    结合所给材料回答问题：
    （1）从一、二、三等舱乘客的幸存率，你能得出什么结论；从男人、女人、儿童、船员的幸存率，你能得出什么结论；写出一条不同于以上两条，你认为有意义的结论；
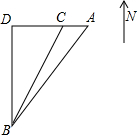    （2）假设B点是“泰坦尼克号”事故地点，在A点的三艘船只收到求救信号后立即前去营救：1号船从A点直线驶向B点；2号船先向西行驶到C点，再直线前往B点；3号先向西行驶100海里到B点正北方D点，再直线前往B点．搜救时海上刮正东风，三艘船顺风行驶速度都是24海里/时，非顺风速度都是12海里/时，若∠BAD=45°，∠BCD=60°，三艘船同时从A点出发，请说明谁先到达营救地点B．（参考数据：
    		2
    ≈1.4，
    		3
    ≈1.7）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    小红、小明、小芳在一起做游戏时，需要确定游戏的先后顺序．他们约定用“剪子、包袱、锤子”的方式确定．问在一个回合中三个人都出包袱的概率是（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了（a+b）n（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）2=a2+2ab+b2展开式中的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）3=a3+3a2b+3ab2+b2展开式中的系数等等．

    （1）根据上面的规律，则（a+b）5的展开式=
    a5+5a4b+10a3b2+10a2b3+5ab4+b5
    a5+5a4b+10a3b2+10a2b3+5ab4+b5
    ．
    （2）利用上面的规律计算：25-5×24+10×23-10×22+5×2-1=
    1
    1
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    在数轴上的三点A、B、C，点A、B对应的数分别是-1，4，点C到点B的距离为2，则点C到点A的距离是
    3或7
    3或7
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    某学校计划利用一片空地建一个学生自行车车棚，自行车车棚为矩形，其中一面靠墙，这堵墙的长度为12米，另三面墙用现有的木板材料围成，总长为26米，且计划建造车棚的面积为80平方米．
    （1）如图1，为了方便学生出行，学校决定在与墙平行的一面开一个2米宽的门，那么这个车棚的长和宽分别应为多少米？
    （2）如图2，为了方便学生取车，施工单位又决定在车棚内修建三条等宽的小路（小路垂直或平行于墙），使得停放自行车的面积为54平方米，那么小路的宽度是多少米？

    查看答案和解析>>

    科目：czsx 来源： 题型：

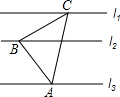    如图，已知△ABC中，∠ABC=90°，AB=BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1，l2之间的距离为2，l2，l3之间的距离为3，则△ABC面积为（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    9、在日历上，三个相邻数（列）的和为54，求这三天分别是几号？
    解：设中间一个数为x，则其余两个分别为
    x-7
    和
    x+7

    依题意得：
    （x-7）+x+（x+7）=54

    解方程得：x=
    18

    ∴x-7=
    11
    x+7=
    25

    答：这三天分别是
    11，18，25
    ．

    查看答案和解析>>