
科目:czsx 来源: 题型:
 34、如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球?请画出A球经过的路线,并写出作法.
34、如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球?请画出A球经过的路线,并写出作法.科目:czsx 来源:2012人教版八年级上 12.2 作轴对称图形 练习题(带解析) 题型:解答题
如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球?请画出A球经过的路线,并写出作法.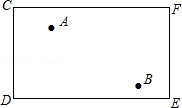
科目:czsx 来源:2012人教版八年级上 12.2 作轴对称图形 练习题(解析版) 题型:解答题
如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球?请画出A球经过的路线,并写出作法.
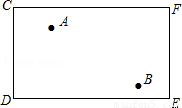
科目:czsx 来源: 题型:解答题
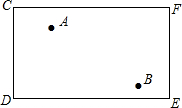 如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球?请画出A球经过的路线,并写出作法.
如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球?请画出A球经过的路线,并写出作法.科目:czsx 来源: 题型:044
如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球?请画出A球经过的路线,并写出作法.

科目:czsx 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:czsx 来源: 题型:
 如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.
如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.科目:czsx 来源: 题型:
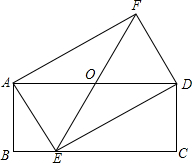 如图,在矩形ABCD中,点O是边AD上的中点,点E是边BC上的一个动点,延长EO到F,使得OE=OF.
如图,在矩形ABCD中,点O是边AD上的中点,点E是边BC上的一个动点,延长EO到F,使得OE=OF.科目:czsx 来源: 题型:
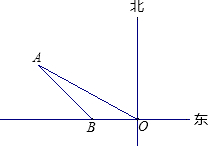 如图,某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行( )
如图,某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行( )A、10(
| ||
B、10(
| ||
C、20(
| ||
D、20(
|
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
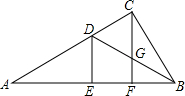 如图所示,Rt△ABC中,CF是斜边AB上的高,角平分线BD交CF于点G,DE⊥AB于点E,则下列结论:①∠A=∠BCF;②CD=CG;③AD=BD;④BC=BE.正确结论的序号
如图所示,Rt△ABC中,CF是斜边AB上的高,角平分线BD交CF于点G,DE⊥AB于点E,则下列结论:①∠A=∠BCF;②CD=CG;③AD=BD;④BC=BE.正确结论的序号科目:czsx 来源: 题型:
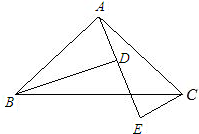 已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E.
已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E.科目:czsx 来源: 题型:
 如图所示,已知C、D是线段AB上的两个点,M、N分别为AC、BD的中点.
如图所示,已知C、D是线段AB上的两个点,M、N分别为AC、BD的中点.