—2x32等于多少答案解析

科目：czsx 来源： 题型：

操作探究：图1a是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图1b的形状拼成一个正方形．
（1）你认为图1b中的阴影部分的正方形的边长等于多少？

m-n

m-n

（2）请用两种不同的方法求图1b中阴影部分的面积．

方法1：

（m-n）²

（m-n）²

；
方法2：

（m+n）²-4mn

（m+n）²-4mn

；
（3）观察图1b你能写出下列三个代数式之间的等量关系吗？代数式：（m+n）²，（m-n）²，mn．

（m-n）²=（m+n）²-4mn

（m-n）²=（m+n）²-4mn

；
（4）根据（3）题中的等量关系，解决如下问题：若a+b=7，ab=5，求（a-b）²的值．
（5）已知：如图2，现有的a×a，b×b正方形和a×b的矩形纸片若干块，试选用这些纸片（每种至少用一次）在如图3的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，作出的图中必须保留拼图的痕迹），使拼出的矩形面积为2a²+5ab+2b²，并标出此矩形的长和宽．

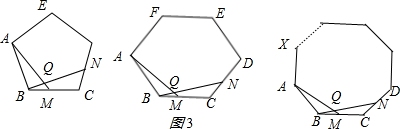
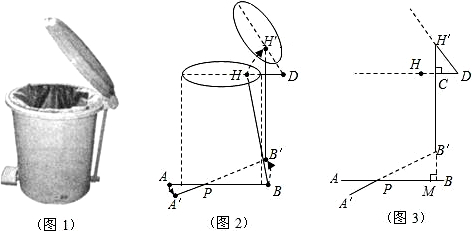
科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

如图所示，直线a、b都垂直于直线c，直线d与a、b相交，如果∠1=72°，那么∠3、∠4等于多少度？

科目：czsx 来源： 题型：

如图，在△ABC中，∠BAC=135°，AD⊥BC，BD=4，DC=6，则△ABC的面积等于多少？

科目：czsx 来源： 题型：

25、如图①是一个长为2a，宽为2b的长方形，沿图中虚线剪开，将其分成4个小长方形，然后按图②的形状拼成一个正方形．

（1）图②中阴影部分的正方形的边长等于多少？
（2）用两种不同的方法求图②中阴影部分的面积．
（3）由图②你能写出下列三个代数式间的关系吗？
（a+b）²，（a-b）²，4ab

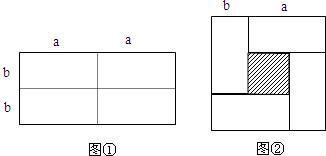
科目：czsx 来源： 题型：

如图，已知梯形ABCD中，DC∥AB，∠A=90°，∠B=60°，AD=3，AB=5

3

，DC=4

3

，P是BC边上一点（P与B不重合），过点P作PQ⊥BC交AB于Q，设PB=x，四边形AQPD的面积为y．
（1）求y与x的函数关系式；
（2）当x为何值时，y有最大值或最小值？其值等于多少？

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

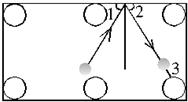22、打台球，我会，看我打得准不准．
如图所示，选择适当的方向击打白球，可以使白球反弹后将红球撞入袋中，此时∠1=∠2，并且∠2+∠3=90°，如果红球与洞口连线和台球桌面边缘夹角∠3=30°，那么∠1应等于多少度，才能保证红球能直接入袋？此时的∠1与∠3是什么关系？

科目：czsx 来源： 题型：

如图，两个半圆中，长为4的弦，AB与直径CD平行且与小半圆相切，那么图中阴影部分的面积等于多少？

科目：czsx 来源： 题型：

62、如图所示，一艘船从A点出发，沿东北方向航行至B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC等于多少

60

度．

科目：czsx 来源： 题型：

如图，在等腰梯形ABCD中，AD∥BC，AB=DC=5，AD=6，BC=12．动点P从D点出发沿DC以每秒1个单位的速度向终点C运动，动点Q从C点出发沿CB以每秒2个单位的速度向B点运动．两点同时出发，当P点到达C点时，Q点随之停止运动．运动时间为t秒．
（1）当PQ∥AB时，P点离开D点的时间等于多少秒？
（2）设五边形ABQPD的面积为S，写出S与t的函数关系式．
（3）PQ能否平分梯形ABCD，说明理由．
（4）当t为何值时，P、Q、C三点构成直角三角形．

科目：czsx 来源： 题型：

如图，已知AB∥CD，∠A=100°，CB平分∠ACD．回答下列问题：
（1）∠ACD等于多少度？为什么？
（2）∠ACB、∠BCD 各等于多少度？为什么？
（3）∠ABC等于多少度？为什么？

科目：czsx 来源： 题型：

在三角形ABC中DE平行于BC，DE交AB于D交AC于E，如果AE=3，EC=5，DE=6，那么BC等于多少？（　　）

A．10

B．16

C．12

D． 18 5

科目：czsx 来源： 题型：

如图1，点P是线段MN的中点．
（1）请你利用该图1画一对以点P为对称中心的全等三角形；
（2）请你参考这个作全等三角形的方法，解答下列问题：
①如图2，在Rt△ABC中，∠BAC=90°，AB＞AC，点D是BC边中点，过D作射线交AB于E，交CA延长线于F，请猜想∠F等于多少度时，BE=CF（直接写出结果，不必证明）；
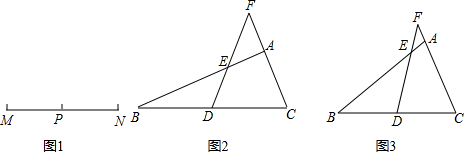②如图3，在△ABC中，如果∠BAC不是直角，而（1）中的其他条件不变，若BE=CF的结论仍然成立，请写出△AEF必须满足的条件，并加以证明．

科目：czsx 来源： 题型：

如图，等腰梯形ABCD中，AD∥BC，AB=AD=DC，∠B=60°，DE∥AB，梯形ABCD的周长等于20cm，则DE等于多少？

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

如图1，图2，是一款家用的垃圾桶，踏板AB（与地面平行）或绕定点P（固定在垃圾桶底部的某一位置）上下转动（转动过程中始终保持AP=A′P，BP=B′P）．通过向下踩踏点A到A′（与地面接触点）使点B上升到点B′，与此同时传动杆BH运动到B'H'的位置，点H绕固定点D旋转（DH为旋转半径）至点H'，从而使桶盖打开一个张角∠HDH′．如图3，桶盖打开后，传动杆H′B′所在的直线分别与水平直线AB、DH垂直，垂足为点M、C，设H′C=B′M．测得AP=6cm，PB=12cm，DH′=8cm．要使桶盖张开的角度∠HDH'不小于60°，那么踏板AB离地面的高度至少等于多少cm？（结果保留两位有效数字）（参考数据：

2

≈1.41，

3

≈1.73）

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

（1）已知：如图1，△ABC为正三角形，点M、N分别在BC、CA边上，且BM=CN，BN与AM相交于Q点，试求∠BQM的度数．
解：∵△ABC为正三角形，∴∠ABC=∠ACB=60°，AB=BC．
在△ABM和△BCN中，

. =        . ∠        . =∠        .        . =        .

⇒△ABM≌△BCN（

 

）．
∴∠

 

=∠

 

，
∴∠BQM=∠

 

+∠

 

=∠

 

+∠

 

=

 

°．
（2）如果将（1）中的正三角形改为正方形ABCD（如图2），点M、N分别在BC、CD边上，且BM=CN，BN与AM相交于Q点，那么∠BQM等于多少度呢？说明理由．

（3）如果将（1）中的“正三角形”改为正五边形、正六边形、…、正n边形（如图3），其余条件都不变，请你根据（1）（2）的求解思路，将你推断的结论填入下表：（正多边形的各个内角都相等）

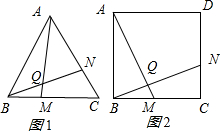
正多边形	正五边形	正六边形	…	正n边形
∠BQM的度数			…