科目：gzsx 来源： 题型：
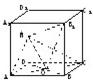已知正方体ABCD-A1B1C1D1的棱长为2，O为AC与BD的交点，M为DD1的中点．科目：gzsx 来源： 题型：
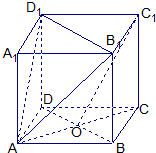已知正方体ABCD-A1B1C1D1，O是底ABCD对角线的交点．求证：科目：gzsx 来源：2006年高考第一轮复习数学：9.11 多面体与正多面体（解析版） 题型：解答题
科目：gzsx 来源： 题型：
(1)求证:平面ACD1∥平面BA1C1;
(2)求证:平面BDD1B1⊥平面BA1C1;
(3)求AC与平面BA1C1间的距离.
科目：gzsx 来源：2010-2011学年山东省济宁市任城一中高二（下）期末数学试卷（文科）（解析版） 题型：解答题
科目：gzsx 来源：安徽省肥西农兴中学2010－2011学年高二上学期期末考试数学理科试题 题型：047
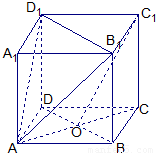
已知正方体ABCD－A1B1C1D1，O是底ABCD对角线的交点．
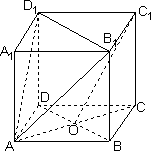
求证：(1)C1O∥面A1B1D1；
(2)A1C⊥面AB1D1；
(3)求直线AC与平面AB1D1所成角的正切值．
科目：gzsx 来源：黄冈重点作业·高二数学（下） 题型：047
如图所示，已知正方体ABCD－A1B1C1D1中，E、F分别为D1C1、B1C1的中点，AC∩BD＝P，A1C1∩EF＝Q．
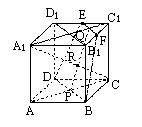
求证：
(1)D、B、F、E四点共面；
(2)若A1C交平面DBFE于R点，则P、Q、R三点共线．
科目：gzsx 来源：2010-2011学年安徽省合肥市肥西县农兴中学高二（上）期末数学试卷（理科）（解析版） 题型：解答题
科目：gzsx 来源：2013届四川省高二下学期期中考试理科数学试卷（解析版） 题型：解答题
已知正方体ABCD－A1B1C1D1，
O是底面ABCD对角线的交点.
（1）求证：A1C⊥平面AB1D1；
（2）求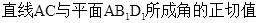
.
【解析】（1）证明线面垂直，需要证明直线垂直这个平面内的两条相交直线，本题只需证：
即可.
（2）可以利用向量法，也可以根据平面A1ACC1与平面AB1D1垂直，可知取B1D1的中点E，则
就是直线AC与平面AB1D1所成的角.然后解三角形即可.
科目：gzsx 来源：安徽省肥西农兴中学2010－2011学年高二上学期期末考试数学文科试题 题型：047
已知正方体ABCD－A1B1C1D1，O是底ABCD对角线的交点．
求证：(1)C1O∥面A1B1D1；
(2)A1C⊥面AB1D1；
(3)求直线AC与平面AB1D1所成角的正切值．
科目：gzsx 来源：同步题 题型：证明题
科目：gzsx 来源：湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型：047
已知正方体ABCD－
中，面对角线A
、B
上分别有两点E、F且E＝F求证：EF∥平面AC．
科目：gzsx 来源：山东省鱼台一中2010－2011学年高二下学期期末考试数学理科试卷 题型：047
已知正方体ABCD－A1B1C1D1，O是底ABCD对角线的交点．
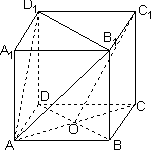
求证：(1)C1O∥面A1B1D1；
(2)A1C⊥面AB1D1；
(3)求直线AC与平面AB1D1所成角的正切值．
科目：gzsx 来源： 题型：
已知正方体ABCD－A1B1C1D1中，E，F分别为D1C1，C1B1的中点，AC∩BD＝P，A1C1∩EF＝Q.求证：
(1)D，B，E，F四点共面；
(2)若A1C交平面BDEF于R点，则P，Q，R三点共线．
科目：gzsx 来源： 题型：
(1)D、B、F、E四点共面；
(2)若直线A1C交平面DBFE于点R，则P、Q、R三点共线.
科目：gzsx 来源：四川省南山中学2011－2012学年高二下学期期中考试数学理科试题 题型：044
已知正方体ABCD－A1B1C1D1，O是底面ABCD对角线的交点．
(1)求证：A1C⊥平面AB1D1；
(2)求直线AC与平面AB1D1所成角的正切值．
科目：gzsx 来源： 题型：
已知正方体ABCD－A1B1C1D1中，E，F分别为D1C1，C1B1的中点，AC∩BD＝P，A1C1∩EF＝Q.求证：
(1)D，B，E，F四点共面；
(2)若A1C交平面BDEF于R点，则P，Q，R三点共线．
如图，已知正方体ABCD-A1B1C1D1；
