分析:本题的两问是递进式的,第(1)问是为第(2)问作铺垫的.第(2)问中构造二面角的平面角的方法是典型的三垂线法.
(1)证明直线与平面垂直,关键要找到两条相交直线与之都垂直.有时候题目中没有现成的直线与直线垂直,需要我们先通过直线与平面垂直去转化一下,如欲证B1O⊥AC,可以先证明AC⊥平面BB1O
(2)二面角的度量关键在于找出它的平面角,构造平面角常用的方法就是三垂线法.
解答:1)证明:∵BB
1⊥平面ABCD,OB⊥AC,
∴B
1O⊥AC.
连接MO、MB
1,则MO=
,B
1O=
,MB
1=3.
∵MO
2+B
1O
2=MB
12,∴∠MOB
1=90°.
∴B
1O⊥MO.
∵MO∩AC=O,∴B
1O⊥平面MAC.
(2)解:作ON⊥AM于点N,连接B
1N.
∵B
1O⊥平面MAC,∴AM⊥平面B
1ON.
∴B
1N⊥AM.
∴∠B
1NO就是二面角B
1-MA-C的平面角.
∵AM=
,CM=
,∴AM=CM.
又O为AC的中点,∴OM⊥AC.则ON=OAsin∠MAO=
•=
.
在Rt△B
1ON中,tan∠B
1NO=
=
,
∴∠B
1NO=arctan
,即所求二面角的大小为arctan
.
点评:证明直线与直线垂直常用的方法有勾股定理、通过直线与平面垂直转化,三垂线定理,其中在立体几何证明垂直的问题中,三垂线定理应用很多,本题的两问都是三垂线定理的应用实例.

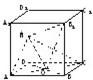 已知正方体ABCD-A1B1C1D1的棱长为2,O为AC与BD的交点,M为DD1的中点.
已知正方体ABCD-A1B1C1D1的棱长为2,O为AC与BD的交点,M为DD1的中点.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=