
科目:czsx 来源: 题型:
| 3 | 2 |
科目:czsx 来源:广东省期中题 题型:解答题
 =_________,1﹣4=_________,
=_________,1﹣4=_________,科目:czsx 来源: 题型:填空题
 =________,1-4=________,(-1)2007=________.
=________,1-4=________,(-1)2007=________.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:阅读理解
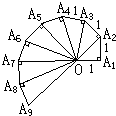 在课本的阅读材料中,介绍了一个第七届国际数学教育大会的会徽.它的主题图案是由一连串如图所示的直角三角形演化而成的.设其中的第一个直角三角形OA1A2是等腰三角形,且OA1=A1A2=A2A3=A3A4=…=A8A9=1,
在课本的阅读材料中,介绍了一个第七届国际数学教育大会的会徽.它的主题图案是由一连串如图所示的直角三角形演化而成的.设其中的第一个直角三角形OA1A2是等腰三角形,且OA1=A1A2=A2A3=A3A4=…=A8A9=1,科目:czsx 来源: 题型:解答题
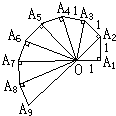 在课本的阅读材料中,介绍了一个第七届国际数学教育大会的会徽.它的主题图案是由一连串如图所示的直角三角形演化而成的.设其中的第一个直角三角形OA1A2是等腰三角形,且OA1=A1A2=A2A3=A3A4=…=A8A9=1,
在课本的阅读材料中,介绍了一个第七届国际数学教育大会的会徽.它的主题图案是由一连串如图所示的直角三角形演化而成的.设其中的第一个直角三角形OA1A2是等腰三角形,且OA1=A1A2=A2A3=A3A4=…=A8A9=1,科目:czsx 来源: 题型:解答题
科目:czsx 来源:江苏期中题 题型:解答题
 的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手。
的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手。 = ( );
= ( );  =( );……
=( );……  =( );
=( );

科目:czsx 来源:江苏期中题 题型:解答题
科目:czsx 来源:2006年广东省佛山市南海区石门实验学校中考数学模拟试卷(解析版) 题型:解答题
科目:czsx 来源:不详 题型:解答题
科目:czsx 来源: 题型:
-b±
| ||
| 2a |
科目:czsx 来源: 题型:
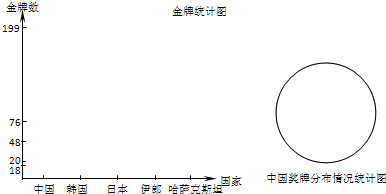
| 中国 | 韩国 | 日本 | 伊郎 | 哈萨克斯坦 | |
| 金牌 | 199 | 76 | 48 | 20 | 18 |
| 银牌 | 119 | 65 | 74 | 14 | 23 |
| 铜牌 | 98 | 119 | 94 | 25 | 38 |
| 合计 | 416 | 232 | 216 | 59 | 79 |
科目:czsx 来源: 题型:022
有理数的混合运算的运算顺序是先做________,再做________,最后做________;同级运算要按________的顺序依次计算;如果有括号,则先计算括号内的数;但若能运用________律,可改变________,使运算简便.
科目:czsx 来源: 题型:解答题
| 中国 | 韩国 | 日本 | 伊郎 | 哈萨克斯坦 | |
| 金牌 | 199 | 76 | 48 | 20 | 18 |
| 银牌 | 119 | 65 | 74 | 14 | 23 |
| 铜牌 | 98 | 119 | 94 | 25 | 38 |
| 合计 | 416 | 232 | 216 | 59 | 79 |

科目:czsx 来源:湖南省期末题 题型:解答题



科目:czsx 来源:不详 题型:解答题
| 中国 | 韩国 | 日本 | 伊郎 | 哈萨克斯坦 | |
| 金牌 | 199 | 76 | 48 | 20 | 18 |
| 银牌 | 119 | 65 | 74 | 14 | 23 |
| 铜牌 | 98 | 119 | 94 | 25 | 38 |
| 合计 | 416 | 232 | 216 | 59 | 79 |

科目:czsx 来源: 题型:填空题
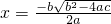 )解一元二次方程时,一般要先计算b2-4ac的值.请问用公式法解一元二次方程-x2+5x=3时b2-4ac的值为 ________.
)解一元二次方程时,一般要先计算b2-4ac的值.请问用公式法解一元二次方程-x2+5x=3时b2-4ac的值为 ________.科目:czsx 来源: 题型:阅读理解
科目:czsx 来源: 题型: